Question

下圖是一個二次函數y=f(x)的圖象，試求這個函數的解析式.

Answer 1

思路解析：二次函數解析式常用的有三種形式：

（1）一般式：y=ax²+bx+c(a、b、c為常數，a≠0)；

（2）頂點式：y=a(x-h)²+k(a、h、k為常數，a≠0)；

（3）兩根式：y=a(x-x₁)(x-x₂)(a、x₁、x₂為常數，a≠0).

要確定二次函數的解析式，就是確定解析式中的待定系數（常數），由于每一種形式都含有三個待定系數，所以用待定系數法求二次函數解析式，需要已知三個獨立的條件.

當已知拋物線上任意三點時，通常設函數的解析式為一般式y=ax²+bx+c，然后列三元一次方程組求解；

當已知拋物線的頂點坐標(h,k)和拋物線上另一點時，通常設函數的解析式為頂點式y=a(x-h)²+k求解；

當已知拋物線與x軸的兩個交點(x₁,0),(x₂,0)時，通常設函數的解析式為y=a(x-x₁)(x-x₂).

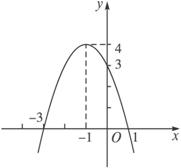
解法一：設y=ax²+bx+c，然后把(-3,0),(1,0)，(-1,4)代入解析式得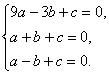解得a=-1,b=-2,c=3.∴所求二次函數為y=-x²-2x+3.

解法二：∵二次函數與x軸有兩個交點(-3,0),(1,0)，∴可設y=a(x+3)(x-1).再把（-1，4）代入，得2×(-2)×a=4,∴a=-1.

∴所求二次函數為y=-(x+3)(x-1)，即為y=-x²-2x+3.

解法三：∵拋物線的頂點為(-1,4)，

∴可設y=a(x+1)²+4，

再把(1,0)代入得4a+4=0,a=-1.

∴所求二次函數為y=-(x+1)²+4，即y=-x²-2x+3.