
【題目】已知橢圓![]() 的對稱軸為坐標軸,離心率為
的對稱軸為坐標軸,離心率為![]() ,且一個焦點坐標為
,且一個焦點坐標為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,以線段
兩點,以線段![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,其中點
,其中點![]() 在橢圓
在橢圓![]() 上,
上, ![]() 為坐標原點,求點
為坐標原點,求點![]() 到直線
到直線![]() 的距離的最小值.
的距離的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:
(1)由題意可求得![]() ,
, ![]() ,∴橢圓
,∴橢圓![]() 的方程為
的方程為![]() .
.
(2)首先討論斜率存在的情況,點![]() 到直線
到直線![]() 的距離的最小值為
的距離的最小值為![]() .
.
當斜率不存在時額外討論可得結論.
試題解析:
解:(1)由已知設橢圓![]() 的方程為
的方程為![]() ,則
,則![]() .
.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,∴橢圓
,∴橢圓![]() 的方程為
的方程為![]() .
.
(2)當直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() 的方程為
的方程為![]() .
.
則由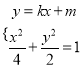 消去
消去![]() 得
得![]() .
.
![]() .①
.①
設點![]() ,
, ![]() ,
, ![]() 的坐標分別是
的坐標分別是![]() ,
, ![]() ,
, ![]() .
.
∵四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,
,
![]() ,
,
由于點![]() 在橢圓
在橢圓![]() 上,∴
上,∴![]() ,
,
從而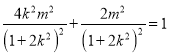 ,化簡得
,化簡得![]() ,經檢驗滿足①式.
,經檢驗滿足①式.
又點![]() 到直線
到直線![]() 的距離為
的距離為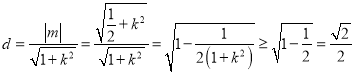 .
.
當且僅當![]() 時,等號成立.
時,等號成立.
當直線![]() 斜率不存在時,由對稱性知,點
斜率不存在時,由對稱性知,點![]() 一定在
一定在![]() 軸上,
軸上,
從而點![]() 的坐標為
的坐標為![]() 或
或![]() ,直線
,直線![]() 的方程為
的方程為![]() ,∴點
,∴點![]() 到直線
到直線![]() 的距離為1.
的距離為1.
∴點![]() 到直線
到直線![]() 的距離的最小值為
的距離的最小值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓![]() 恰好經過橢圓
恰好經過橢圓![]() 的兩個焦點和兩個頂點.
的兩個焦點和兩個頂點.
(1)求橢圓![]() 的方程;
的方程;
(2)經過原點的直線![]() (不與坐標軸重合)交橢圓
(不與坐標軸重合)交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 軸,垂足為
軸,垂足為![]() ,連接
,連接![]() 并延長
并延長![]() 交橢圓
交橢圓![]() 于
于![]() ,證明:以線段
,證明:以線段![]() 為直徑的圓經過點
為直徑的圓經過點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有芻甍,下廣三丈,袤四丈,上袤二丈,無廣,高二丈,問積幾何?”其意思為:“今有底面為矩形的屋脊狀的鍥體,下底面寬3丈,長4丈,上棱長2丈,高2丈,問:它的體積是多少?”已知1丈為10尺,該鍥體的三視圖如圖所示,則該鍥體的體積為( )
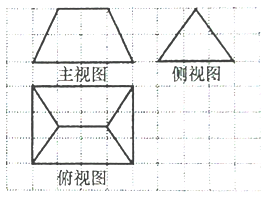
A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,氣象部門預報,在海面上生成了一股較強臺風,在據臺風中心60千米的圓形區域內將受到嚴重破壞,臺風中心這個從海岸M點登陸,并以72千米/小時的速度沿北偏西60°的方向移動,已知M點位于A城的南偏東15°方向,距A城 ![]() 千米;M點位于B城的正東方向,距B城
千米;M點位于B城的正東方向,距B城 ![]() 千米,假設臺風在移動的過程中,其風力和方向保持不變,請回答下列問題:
千米,假設臺風在移動的過程中,其風力和方向保持不變,請回答下列問題: 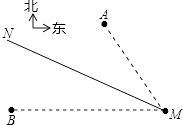
(1)A城和B城是否會受到此次臺風的侵襲?并說明理由;
(2)若受到此次臺風的侵襲,改城受到臺風侵襲的持續時間有多少小時?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com