
拋物線 的準線與
的準線與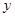 軸交于
軸交于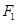 ,焦點為
,焦點為 ,若橢圓
,若橢圓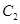 以
以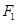 、
、 為焦點、
為焦點、
且離心率為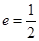 。
。
(1)當 時求橢圓
時求橢圓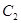 的方程;
的方程;
(2)若拋物線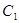 與直線
與直線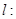
 及
及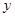 軸所圍成的圖形的面積為
軸所圍成的圖形的面積為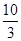 ,求拋物線
,求拋物線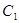 和直線
和直線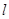 的方程
的方程
(1) (2)拋物線方程為
(2)拋物線方程為 ,直線方程為
,直線方程為
【解析】本試題主要是考查了拋物線的性質和橢圓的方程的求解以及直線與拋物線的位置關系的綜合運用。
(1)因為已知題意的離心率和拋物線的方程得到準線方程,進而得到焦點坐標,得到c的值,從而借助于a,b,c關系式得到橢圓的方程。
(2)聯立直線與拋物線方程,那么可知方程的解,進而得到圍成的圖形的面積的定積分,求解得到n的值,解決問題。
(1)當 時,拋物線
時,拋物線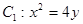 的準線為
的準線為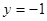 ,則
,則 ,……2分
,……2分
假設橢圓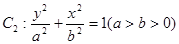 ,則
,則 ,離心率
,離心率 ……2分
……2分
故 ,
,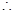 此時橢圓
此時橢圓 的方程為
的方程為 ……2分
……2分
(2)由 消
消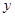 得:
得: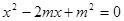 ,解得
,解得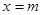 ……2分
……2分
故所圍成的圖形的面積
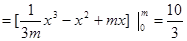
解得: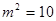 ,又
,又 ,
,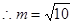 ,
,
所以:拋物線方程為 ,直線方程為
,直線方程為


科目:高中數學 來源: 題型:
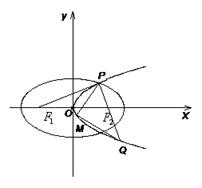
如圖,設拋物線![]() 的準線與
的準線與![]() 軸交于
軸交于![]() ,焦點為
,焦點為![]() ;以
;以![]() 為焦點,離心率
為焦點,離心率![]() 的橢圓
的橢圓![]() 與拋物線
與拋物線![]() 在
在![]() 軸上方的交點為
軸上方的交點為![]() ,延長
,延長![]() 交拋物線于點
交拋物線于點![]() ,
,![]() 是拋物線
是拋物線![]() 上一動點,且M在
上一動點,且M在![]() 與
與![]() 之間運動.
之間運動.
(1)當![]() 時,求橢圓
時,求橢圓![]() 的方程;
的方程;
(2)當![]() 的邊長恰好是三個連續的自然數時,求
的邊長恰好是三個連續的自然數時,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源:2014屆山西省高二下學期期中考試數學理科試卷(解析版) 題型:解答題
拋物線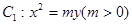 的準線與
的準線與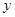 軸交于
軸交于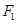 ,焦點為
,焦點為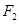 ,若橢圓
,若橢圓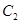 以
以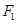 、
、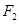 為焦點、且離心率為
為焦點、且離心率為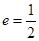 .
.
(1)當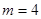 時,求橢圓
時,求橢圓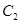 的方程;
的方程;
(2)若拋物線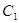 與直線
與直線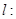
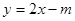 及
及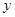 軸所圍成的圖形的面積為
軸所圍成的圖形的面積為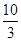 ,求拋物線
,求拋物線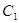 和直線
和直線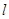 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年四川省高考壓軸理科數學試卷(解析版) 題型:選擇題
設拋物線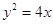 的準線與
的準線與 軸交于
軸交于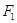 ,焦點為
,焦點為 ,以
,以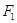 ,
, 為焦點,離心率為
為焦點,離心率為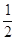 的橢圓的兩條準線之間的距離為 ( )
的橢圓的兩條準線之間的距離為 ( )
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:高中數學 來源:2012屆河北省唐山市高三年級第一學期期末考試理科數學試卷(解析版) 題型:解答題
(本小題滿分12分)已知拋物線 的焦點為F,過點F作直線
的焦點為F,過點F作直線 與拋物線交于A,B兩點,拋物線的準線與
與拋物線交于A,B兩點,拋物線的準線與 軸交于點C。
軸交于點C。
(1)證明: ;
;
(2)求 的最大值,并求
的最大值,并求 取得最大值時線段AB的長。
取得最大值時線段AB的長。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河北省高三上學期第三次考試理科數學卷 題型:選擇題
設拋物線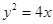 的準線與
的準線與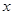 軸交于
軸交于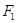 ,焦點為
,焦點為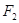 ,以
,以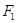 ,
,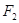 為焦點,離心率為
為焦點,離心率為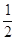 的橢圓的兩條準線之間的距離為
的橢圓的兩條準線之間的距離為
A.4 B.6 C.8 D.10
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com