
【題目】設數列![]() 的前
的前![]() 項的和為
項的和為![]() 且
且![]() 數列
數列![]() 滿足
滿足![]() 且對任意正整數
且對任意正整數![]() 都有
都有![]() 成等比數列.
成等比數列.
(1)求數列![]() 的通項公式.
的通項公式.
(2)證明數列![]() 為等差數列.
為等差數列.
(3)令![]() 問是否存在正整數
問是否存在正整數![]() 使得
使得![]() 成等比數列?若存在,求出
成等比數列?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(1)![]() (2)見證明;(3)見證明
(2)見證明;(3)見證明
【解析】
(1)利用項和公式求數列![]() 的通項公式.(2)由題得
的通項公式.(2)由題得![]() ,
,![]() ,即
,即![]() ,再求出
,再求出![]() ,再利用等差數列的定義證明數列
,再利用等差數列的定義證明數列![]() 為等差數列.(3) 先求出
為等差數列.(3) 先求出![]() ,所以
,所以![]() ,根據
,根據![]() 成等比數列得
成等比數列得![]() ,即
,即![]() ,再求出m,k的值.
,再求出m,k的值.
(1)因為數列![]() 的前
的前![]() 項的和
項的和![]() ,
,
所以當![]() 時,
時,![]() ;
;
當![]() 且
且![]() 時,
時,![]() ,
,
當![]() 時,上式也成立,
時,上式也成立,
所以數列![]() 的通項公式為
的通項公式為![]() .
.
(2)證明:因為對任意正整數![]() 都有
都有![]() 成等比數列,
成等比數列,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
兩式相除得,對任意正整數![]() 都有
都有![]() ,
,
即![]() ,
,
當![]() 為奇數時,
為奇數時,![]() ,所以
,所以![]() ,
,
當![]() 為偶數時,
為偶數時,![]() ,而
,而![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以![]() ,
,
所以數列![]() 為等差數列.
為等差數列.
(3)因為![]() ,
,
所以![]() ,
,
因此存在正整數![]() ,使得
,使得![]() 成等比數列
成等比數列
![]()
![]() ,
,
![]()
因為![]() 都是正整數,則
都是正整數,則![]() ,
,
即![]() 時,對應的
時,對應的![]() .
.
所以存在![]() 或
或![]() 或
或![]() 使得
使得![]() 成等比數列.
成等比數列.


科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元.為增加企業競爭力,決定優化產業結構,調整出![]() 名員工從事第三產業,調整后平均每人每年創造利潤為
名員工從事第三產業,調整后平均每人每年創造利潤為![]() 萬元
萬元![]() ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高![]() .
.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(2)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下,若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,則![]() 的取值范圍是多少?
的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
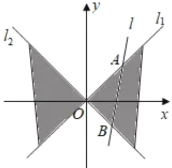
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與直線
與直線![]() 之間的陰影部分記為
之間的陰影部分記為![]() ,區域
,區域![]() 中動點
中動點![]() 到
到![]() 的距離之積為1.
的距離之積為1.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)對于區域![]() 中動點
中動點![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)動直線![]() 穿過區域
穿過區域![]() ,分別交直線
,分別交直線![]() 于
于![]() 兩點,若直線
兩點,若直線![]() 與點
與點![]() 的軌跡
的軌跡![]() 有且只有一個公共點,求證:
有且只有一個公共點,求證:![]() 的面積值為定值.
的面積值為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象的頂點坐標為
的圖象的頂點坐標為![]() ,且過坐標原點
,且過坐標原點![]() .數列
.數列![]() 的前
的前![]() 項和為
項和為![]() ,點
,點![]() 在二次函數
在二次函數![]() 的圖象上.
的圖象上.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,若
,若![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)在數列![]() 中是否存在這樣一些項:
中是否存在這樣一些項:![]()
![]()
![]() ,這些項都能夠構成以
,這些項都能夠構成以![]() 為首項,
為首項,![]() 為公比的等比數列
為公比的等比數列![]() ?若存在,寫出
?若存在,寫出![]() 關于
關于![]() 的表達式;若不存在,說明理由.
的表達式;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
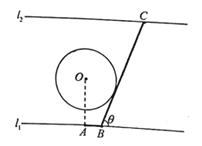
【題目】如圖為某大河的一段支流,岸線![]() 近似滿足
近似滿足![]() ∥
∥![]() 寬度為7
寬度為7![]() 圓
圓![]() 為河中的一個半徑為2
為河中的一個半徑為2![]() 的小島,小鎮
的小島,小鎮![]() 位于岸線
位于岸線![]() 上,且滿足岸線
上,且滿足岸線![]() 現計劃建造一條自小鎮
現計劃建造一條自小鎮![]() 經小島
經小島![]() 至對岸
至對岸![]() 的通道
的通道![]() (圖中粗線部分折線段,
(圖中粗線部分折線段,![]() 在
在![]() 右側),為保護小島,
右側),為保護小島,![]() 段設計成與圓
段設計成與圓![]() 相切,設
相切,設![]()
(1)試將通道![]() 的長
的長![]() 表示成
表示成![]() 的函數,并指出其定義域.
的函數,并指出其定義域.
(2)求通道![]() 的最短長.
的最短長.
查看答案和解析>>
科目:高中數學 來源: 題型:
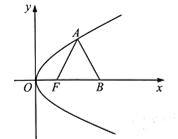
【題目】在平面直角坐標系![]() 中,已知點F為拋物線
中,已知點F為拋物線![]() 的焦點,點A在拋物線E上,
的焦點,點A在拋物線E上,
點B在x軸上,且![]() 是邊長為2的等邊三角形。
是邊長為2的等邊三角形。
(1)求拋物線E的方程;
(2)設C是拋物線E上的動點,直線![]() 為拋物線E在點C處的切線,求點B到直線
為拋物線E在點C處的切線,求點B到直線![]() 距離的最小值,并求此時點C的坐標。
距離的最小值,并求此時點C的坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:
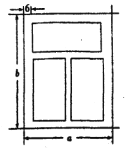
【題目】如圖,一個鋁合金窗分為上、下兩欄,四周框架和中間隔檔的材料為鋁合金,寬均為6![]() ,上欄與下欄的框內高度(不含鋁合金部分)的比為1:2,此鋁合金窗占用的墻面面積為28800
,上欄與下欄的框內高度(不含鋁合金部分)的比為1:2,此鋁合金窗占用的墻面面積為28800![]() ,設該鋁合金窗的寬和高分別為
,設該鋁合金窗的寬和高分別為![]() ,鋁合金窗的透光部分的面積為
,鋁合金窗的透光部分的面積為![]() .
.
(1)試用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,則鋁合金窗的寬和高分別為多少?
最大,則鋁合金窗的寬和高分別為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com