
【題目】已知函數(shù)![]() .
.
(1)求![]() 在
在![]() 上的最值;
上的最值;
(2)設(shè)![]() ,若當(dāng)
,若當(dāng)![]() ,且
,且![]() 時(shí),
時(shí),![]() ,求整數(shù)
,求整數(shù)![]() 的最小值..
的最小值..
【答案】(1)詳見解析(2)2
【解析】
(1)先對(duì)函數(shù)求導(dǎo),然后討論參數(shù)![]() 的范圍,分別判斷每種情況下
的范圍,分別判斷每種情況下![]() 的單調(diào)性,即可求出對(duì)應(yīng)的最值;
的單調(diào)性,即可求出對(duì)應(yīng)的最值;
(2)先寫出![]() 的解析式,分兩種情況討論:
的解析式,分兩種情況討論:
當(dāng)![]() 時(shí),由(1)易知
時(shí),由(1)易知![]() 時(shí),
時(shí),![]() ,從而
,從而![]() ,進(jìn)而可得m的范圍;
,進(jìn)而可得m的范圍;
當(dāng)![]() 時(shí),可將
時(shí),可將![]() 變形為
變形為![]() ,只需用導(dǎo)數(shù)的方法研究
,只需用導(dǎo)數(shù)的方法研究![]() 的單調(diào)性和最值即可;
的單調(diào)性和最值即可;
解法一:
(1)![]() ,
,
①當(dāng)![]() 時(shí),
時(shí),
因?yàn)?/span>![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() ,無最小值.
,無最小值.
②當(dāng)![]() 時(shí),
時(shí),
令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
所以![]() ,無最大值.
,無最大值.
③當(dāng)![]() 時(shí),
時(shí),
因?yàn)?/span>![]() ,等號(hào)僅在
,等號(hào)僅在![]() ,
,![]() 時(shí)成立,
時(shí)成立,
所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,無最大值.
,無最大值.
綜上,當(dāng)![]() 時(shí),
時(shí),![]() ,無最小值;當(dāng)
,無最小值;當(dāng)![]() 時(shí),
時(shí),![]() ,無最大值;當(dāng)
,無最大值;當(dāng)![]() 時(shí),
時(shí),![]() ,無最大值.
,無最大值.
(2)![]() ,
,
當(dāng)![]() 時(shí),因
時(shí),因![]() 為,由(1)知
為,由(1)知![]() ,所以
,所以![]() (當(dāng)
(當(dāng)![]() 時(shí)等號(hào)成立),所以
時(shí)等號(hào)成立),所以![]() .
.
當(dāng)![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,已知化為
,已知化為![]() 在
在![]() 上恒成立,
上恒成立,
因?yàn)?/span>![]() ,
,
令![]() ,
,![]() ,則
,則![]() ,
,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
又因?yàn)?/span>![]() ,
,![]() ,
,
所以存在![]() 使得
使得![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
所以![]() ,
,
因?yàn)?/span>![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的最小整數(shù)值為2.
的最小整數(shù)值為2.
解法二:
(1)同解法一.
(2)![]() ,
,
①當(dāng)![]() 時(shí),因
時(shí),因![]() 為,由(1)知
為,由(1)知![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
②當(dāng)![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,已知化為
,已知化為![]() 在
在![]() 上恒成立,
上恒成立,
因?yàn)?/span>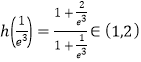 在
在![]() 上,所以
上,所以![]() ,
,
下面證明![]() ,即證
,即證![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,![]() ,
,
則![]() ,令
,令![]() ,得,
,得,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上遞減;
上遞減;
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上遞增,
上遞增,
所以![]() ,且
,且![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() .
.
由①②得當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以![]() 的最小整數(shù)值為2.
的最小整數(shù)值為2.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知球![]() 的半徑為3,該球的內(nèi)接正三棱錐的體積最大值為
的半徑為3,該球的內(nèi)接正三棱錐的體積最大值為![]() ,內(nèi)接正四棱錐的體積最大值為
,內(nèi)接正四棱錐的體積最大值為![]() ,則
,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中藥種植基地有兩處種植區(qū)的藥材需在下周一、下周二兩天內(nèi)采摘完畢,基地員工一天可以完成一處種植區(qū)的采摘.由于下雨會(huì)影響藥材品質(zhì),基地收益如下表所示:
周一 | 無雨 | 無雨 | 有雨 | 有雨 |
周二 | 無雨 | 有雨 | 無雨 | 有雨 |
收益 |
|
|
|
|
若基地額外聘請工人,可在周一當(dāng)天完成全部采摘任務(wù).無雨時(shí)收益為![]() 萬元;有雨時(shí),收益為
萬元;有雨時(shí),收益為![]() 萬元.額外聘請工人的成本為
萬元.額外聘請工人的成本為![]() 萬元.
萬元.
已知下周一和下周二有雨的概率相同,兩天是否下雨互不影響,基地收益為![]() 萬元的概率為
萬元的概率為![]() .
.
(Ⅰ)若不額外聘請工人,寫出基地收益![]() 的分布列及基地的預(yù)期收益;
的分布列及基地的預(yù)期收益;
(Ⅱ)該基地是否應(yīng)該外聘工人,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給定正整數(shù)![]() ,將
,將![]() 分拆成若干個(gè)互異正整數(shù)的和,這些正整數(shù)的乘積記為
分拆成若干個(gè)互異正整數(shù)的和,這些正整數(shù)的乘積記為![]() .對(duì)所有不同的分法,求
.對(duì)所有不同的分法,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知直線
中,已知直線![]() :
: (
(![]() 為參數(shù)).以坐標(biāo)原點(diǎn)
為參數(shù)).以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點(diǎn)![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】北京市政府為做好![]() 會(huì)議接待服務(wù)工作,對(duì)可能遭受污染的某海產(chǎn)品在進(jìn)入餐飲區(qū)前必須進(jìn)行兩輪檢測,只有兩輪都合格才能進(jìn)行銷售,否則不能銷售.已知該海產(chǎn)品第一輪檢測不合格的概率為
會(huì)議接待服務(wù)工作,對(duì)可能遭受污染的某海產(chǎn)品在進(jìn)入餐飲區(qū)前必須進(jìn)行兩輪檢測,只有兩輪都合格才能進(jìn)行銷售,否則不能銷售.已知該海產(chǎn)品第一輪檢測不合格的概率為![]() ,第二輪檢測不合格的概率為
,第二輪檢測不合格的概率為![]() ,兩輪檢測是否合格相互沒有影響.
,兩輪檢測是否合格相互沒有影響.
(1)求該海產(chǎn)品不能銷售的概率.
(2)如果該海產(chǎn)品可以銷售,則每件產(chǎn)品可獲利40元;如果該海產(chǎn)品不能銷售,則每件產(chǎn)品虧損80元(即獲利-80元).已知一箱中有該海產(chǎn)品4件,記一箱該海產(chǎn)品獲利![]() 元,求
元,求![]() 的分布列,并求出數(shù)學(xué)期望
的分布列,并求出數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將圓![]() 上每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉淼?/span>
上每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉淼?/span>![]() ,得曲線
,得曲線![]() .
.
(1)求出![]() 的參數(shù)方程;
的參數(shù)方程;
(2)以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,設(shè)
軸正半軸為極軸建立極坐標(biāo)系,設(shè)![]() 是曲線
是曲線![]() 上的一個(gè)動(dòng)點(diǎn),求點(diǎn)
上的一個(gè)動(dòng)點(diǎn),求點(diǎn)![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等差數(shù)列![]() 中,已知公差
中,已知公差![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列![]() 的通項(xiàng)公式
的通項(xiàng)公式![]() ;
;
(2)求![]() .
.
【答案】(1)![]() ;(2)100
;(2)100
【解析】試題分析:(1)根據(jù)題意![]() ,
, ![]() ,
, ![]() 成等比數(shù)列得
成等比數(shù)列得![]() 得
得![]() 求出d即可得通項(xiàng)公式;(2)求項(xiàng)的絕對(duì)前n項(xiàng)和,首先分清數(shù)列有多少項(xiàng)正數(shù)項(xiàng)和負(fù)數(shù)項(xiàng),然后正數(shù)項(xiàng)絕對(duì)值數(shù)值不變,負(fù)數(shù)項(xiàng)絕對(duì)值要變號(hào),從而得
求出d即可得通項(xiàng)公式;(2)求項(xiàng)的絕對(duì)前n項(xiàng)和,首先分清數(shù)列有多少項(xiàng)正數(shù)項(xiàng)和負(fù)數(shù)項(xiàng),然后正數(shù)項(xiàng)絕對(duì)值數(shù)值不變,負(fù)數(shù)項(xiàng)絕對(duì)值要變號(hào),從而得![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]()
![]()
![]()
![]() 計(jì)算 即可得出結(jié)論
計(jì)算 即可得出結(jié)論
解析:(1)由題意可得,則![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
化簡得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(2)由(1)得![]() 時(shí),
時(shí),
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
∴![]() .
.
點(diǎn)睛:對(duì)于數(shù)列第一問首先要熟悉等差和等比通項(xiàng)公式及其性質(zhì)即可輕松解決,對(duì)于第二問前n項(xiàng)的絕對(duì)值的和問題,首先要找到數(shù)列由多少正數(shù)項(xiàng)和負(fù)數(shù)項(xiàng),進(jìn)而找到絕對(duì)值所影響的項(xiàng),然后在求解即可得結(jié)論
【題型】解答題
【結(jié)束】
18
【題目】甲、乙兩家銷售公司擬各招聘一名產(chǎn)品推銷員,日工資方案如下: 甲公司規(guī)定底薪80元,每銷售一件產(chǎn)品提成1元; 乙公司規(guī)定底薪120元,日銷售量不超過45件沒有提成,超過45件的部分每件提成8元.
(I)請將兩家公司各一名推銷員的日工資![]() (單位: 元) 分別表示為日銷售件數(shù)
(單位: 元) 分別表示為日銷售件數(shù)![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(II)從兩家公司各隨機(jī)選取一名推銷員,對(duì)他們過去100天的銷售情況進(jìn)行統(tǒng)計(jì),得到如下條形圖。若記甲公司該推銷員的日工資為![]() ,乙公司該推銷員的日工資為
,乙公司該推銷員的日工資為![]() (單位: 元),將該頻率視為概率,請回答下面問題:
(單位: 元),將該頻率視為概率,請回答下面問題:
某大學(xué)畢業(yè)生擬到兩家公司中的一家應(yīng)聘推銷員工作,如果僅從日均收入的角度考慮,請你利用所學(xué)的統(tǒng)計(jì)學(xué)知識(shí)為他作出選擇,并說明理由.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com