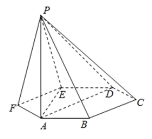
【題目】已知六棱錐
的底面是正六邊形，
平面ABC，
.則下列命題中正確的有（ ）
①平面
平面PAE；
②
；
③直線CD與PF所成角的余弦值為
；
④直線PD與平面ABC所成的角為45°；
⑤
平面PAE.
A.①④B.①③④C.②③⑤D.①②④⑤
【答案】B
【解析】
①要判斷面面垂直，需先判斷是否有線面垂直，根據線線，線面的垂直關系判斷；②由條件可知若
，可推出
平面
，則
，判斷是否有矛盾；
③異面直線所成的角轉化為相交直線所成的角，即根據
，轉化為求
；④根據線面角的定義直接求解；⑤若
平面
，則
，由正六邊形的性質判斷是否有矛盾.
∵
平面ABC，∴
，在正六邊形ABCDEF中，
，
，∴
平面PAE，且
面PAB，
∴平面
平面PAE，故①成立；
由條件可知若，平面
，則
，
，可推出平面，則，這與
不垂直矛盾，故②不成立；
∵
，直線CD與PF所成角為
，
在
中，
，
∴
，∴③成立.
在
中，
，
∴
，故④成立.
若平面，平面
平面
則，這與
不平行矛盾，故⑤不成立.
所以正確的是①③④
故選：B
智趣暑假溫故知新系列答案科目：高中數學 來源： 題型：
【題目】《情境》劉曉紅同學在做達標訓練的課外作業時，遇到一個如何用五點法作出正弦型函數在長度為一個周期的閉區間上的圖象及圖象之間如何進行變換的問題，她犯愁了．
《問題》設函數
的周期為
，且圖象過點
．
（1）求
與
的值；
（2）用五點法作函數
在長度為一個周期的閉區間上的圖象；
（3）敘述函數的圖象可由函數
的圖象經過怎樣的變換而得到．
由于劉曉紅對上述問題還沒有掌握解決方法及解題概念和步驟，導致無從下手，于是她請教了班上的學習委員張倩同學給她做了如下點撥：
用五點法作出在一個周期的閉區間上的圖象，首先要列表并分別令相位
、
、、
、
，再解出對應的
、
的值，得出坐標
，然后描點，最后畫出圖象．而由函數的圖象變到函數
的圖象主要有兩種途徑：①按物理量初相，周期
，振幅
的順序變換；②按物理量周期，初相，振幅的順序變換．要注意兩者操作的區別，防止出錯．
經過張倩耐心而細致的解釋，劉曉紅豁然開朗，并對該題解答如下：
（注意：解答第（3）問時，要按照題中要求，寫出兩種變換過程）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[2019·清遠期末]一只紅鈴蟲的產卵數
和溫度
有關，現收集了4組觀測數據列于下表中，根據數據作出散點圖如下：
溫度 | 20 | 25 | 30 | 35 |
產卵數 | 5 | 20 | 100 | 325 |
（1）根據散點圖判斷
與
哪一個更適宜作為產卵數關于溫度的回歸方程類型？（給出判斷即可，不必說明理由）
（2）根據（1）的判斷結果及表中數據，建立關于的回歸方程（數字保留2位小數）；
（3）要使得產卵數不超過50，則溫度控制在多少
以下？（最后結果保留到整數）
參考數據：
，
，
，
，
，
，
，
，
，
，
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】解答下列問題：
（1）求平行于直線3x+4y- 2=0,且與它的距離是1的直線方程；
（2）求垂直于直線x+3y -5=0且與點P( -1,0)的距離是
的直線方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】依據某地某條河流8月份的水文觀測點的歷史統計數據所繪制的頻率分布直方圖如圖（甲）所示；依據當地的地質構造，得到水位與災害等級的頻率分布條形圖如圖（乙）所示．
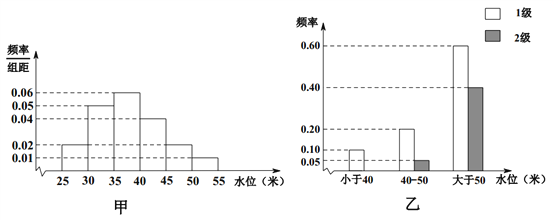
試估計該河流在8月份水位的中位數；
（1）以此頻率作為概率，試估計該河流在8月份發生1級災害的概率；
（2）該河流域某企業，在8月份，若沒受1、2級災害影響，利潤為500萬元；若受1級災害影響，則虧損100萬元；若受2級災害影響則虧損1000萬元．
現此企業有如下三種應對方案：
方案 | 防控等級 | 費用（單位：萬元） |
方案一 | 無措施 | 0 |
方案二 | 防控1級災害 | 40 |
方案三 | 防控2級災害 | 100 |
試問，如僅從利潤考慮，該企業應選擇這三種方案中的哪種方案？說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從甲地到乙地要經過3個十字路口，設各路口信號燈工作相互獨立，且在各路口遇到紅燈的概率分別為
.
（Ⅰ）設
表示一輛車從甲地到乙地遇到紅燈的個數，求隨機變量
的分布列和數學期望；
（Ⅱ）若有2輛車獨立地從甲地到乙地，求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
