
某校為了解學生的學科學習興趣,對初高中學生做了一個喜歡數學和喜歡語文的抽樣調查,隨機抽取了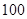 名學生,相關的數據如下表所示:
名學生,相關的數據如下表所示:
|
|
數學 |
語文 |
總計 |
|
初中 |
|
|
|
|
高中 |
|
|
|
|
總計 |
|
|
|
(1) 用分層抽樣的方法從喜歡語文的學生中隨機抽取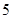 名,高中學生應該抽取幾名?
名,高中學生應該抽取幾名?
(2) 在(1)中抽取的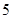 名學生中任取
名學生中任取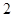 名,求恰有
名,求恰有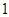 名初中學生的概率.
名初中學生的概率.
(1)3 名
(2) 其中恰有1名初中學生的情況有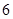 種,它們是:
種,它們是: ,
,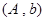 ,
,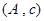 ,
,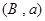 ,
,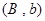 ,
,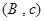 .
.
【解析】試題分析:(1) 由表中數據可知, 高中學生應該抽取高中學生人數乘以高中學生占總人數的比例.
(2)本小題屬于古典概型概率計算問題,先計算出本次試驗總的基本結果的個數,然后再求出事件發生的基本結果的個數.再利用古典概率計算即可.
解:(1)由表中數據可知, 高中學生應該抽取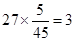 人.…4分
人.…4分
(2) 記抽取的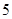 名學生中,初中
名學生中,初中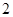 名學生為
名學生為 ,
,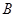 ,高中
,高中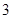 名學生為
名學生為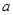 ,
,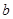 ,
,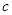 ,
,
則從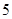 名學生中任取2名的所有可能的情況有
名學生中任取2名的所有可能的情況有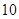 種,它們是:
種,它們是: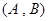 ,
, ,
,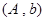 ,
,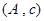 ,
,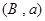 ,
,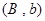 ,
,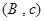 ,
,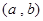 ,
,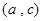 ,
,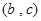 .……7分
.……7分
其中恰有1名初中學生的情況有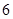 種,它們是:
種,它們是: ,
,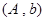 ,
,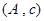 ,
,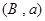 ,
,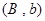 ,
,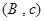 .…9分
.…9分
故所求概率為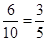 . …12分
. …12分
考點:本小題主要考查分層抽樣、古典概型等知識,考查或然與必然,樣本估計總體的統計思想方法,以及數據觀察能力、抽象思維能力和應用意識.
點評:分層抽樣的規則,各層在總體中的占比與在樣本中的占比相等.
古典概率:第一步求出總的基本結果個數n0,第二步求出事件包含的基本事件的個數n,再根據公式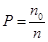 計算概率即可.
計算概率即可.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
 某校為了解學生的學科學習興趣,對初高中學生做了一個喜歡數學和喜歡語文的抽樣調查,隨機抽取了100名學生,相關的數據如下表所示:
某校為了解學生的學科學習興趣,對初高中學生做了一個喜歡數學和喜歡語文的抽樣調查,隨機抽取了100名學生,相關的數據如下表所示:| 數學 | 語文 | 總計 | |
| 初中 | 36 | 14 | 50 |
| 高中 | 24 | 26 | 50 |
| 總計 | 60 | 40 | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 數學 | 語文 | 總計 | |
| 初中 | 40 | 18 | 58 |
| 高中 | 15 | 27 | 42 |
| 總計 | 55 | 45 | 100 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省深圳市高三12月月考文科數學試卷(解析版) 題型:解答題
(12分)某校為了解學生的學科學習興趣,對初高中學生做了一個喜歡數學和喜歡語文的抽樣調查,隨機抽取了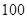 名學生,相關的數據如下表所示:
名學生,相關的數據如下表所示:
|
|
數學 |
語文 |
總計 |
|
初中 |
|
|
|
|
高中 |
|
|
|
|
總計 |
|
|
|
(1) 、用分層抽樣的方法從喜歡語文的學生中隨機抽取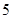 名,高中學生應該抽取幾名?
名,高中學生應該抽取幾名?
(2) 、在(1)中抽取的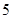 名學生中任取
名學生中任取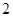 名,求恰有
名,求恰有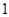 名初中學生的概率.
名初中學生的概率.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省深圳市南頭中學高三(上)12月月考數學試卷(文科)(解析版) 題型:解答題
| 數學 | 語文 | 總計 | |
| 初中 | 36 | 14 | 50 |
| 高中 | 24 | 26 | 50 |
| 總計 | 60 | 40 | 100 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com