
【題目】已知函數f(x)=sin(3x+ ![]() ).
).
(1)求f(x)的單調遞增區間;
(2)若α是第二象限角,f( ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,求cosα﹣sinα的值.
)cos2α,求cosα﹣sinα的值.
【答案】
(1)解:∵函數f(x)=sin(3x+ ![]() ),令 2kπ﹣
),令 2kπ﹣ ![]() ≤3x+
≤3x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
求得 ![]() ﹣
﹣ ![]() ≤x≤
≤x≤ ![]() +
+ ![]() ,故函數的增區間為[
,故函數的增區間為[ ![]() ﹣
﹣ ![]() ,
, ![]() +
+ ![]() ],k∈Z.
],k∈Z.
(2)解:由函數的解析式可得 f( ![]() )=sin(α+
)=sin(α+ ![]() ),又f(
),又f( ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,
)cos2α,
∴sin(α+ ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,即sin(α+
)cos2α,即sin(α+ ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )(cos2α﹣sin2α),
)(cos2α﹣sin2α),
∴sinαcos ![]() +cosαsin
+cosαsin ![]() =
= ![]() (cosαcos
(cosαcos ![]() ﹣sinαsin
﹣sinαsin ![]() )(cosα﹣sinα)(cosα+sinα)
)(cosα﹣sinα)(cosα+sinα)
即 (sinα+cosα)= ![]() (cosα﹣sinα)2(cosα+sinα),
(cosα﹣sinα)2(cosα+sinα),
又∵α是第二象限角,∴cosα﹣sinα<0,
當sinα+cosα=0時,tanα=﹣1,sinα= ![]() ,cosα=﹣
,cosα=﹣ ![]() ,此時cosα﹣sinα=﹣
,此時cosα﹣sinα=﹣ ![]() .
.
當sinα+cosα≠0時,此時cosα﹣sinα=﹣ ![]() .
.
綜上所述:cosα﹣sinα=﹣ ![]() 或﹣
或﹣ ![]()
【解析】(1)令 2kπ﹣ ![]() ≤3x+
≤3x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,求得x的范圍,可得函數的增區間.(2)由函數的解析式可得 f(
,k∈z,求得x的范圍,可得函數的增區間.(2)由函數的解析式可得 f( ![]() )=sin(α+
)=sin(α+ ![]() ),又f(
),又f( ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,可得sin(α+
)cos2α,可得sin(α+ ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,化簡可得 (cosα﹣sinα)2=
)cos2α,化簡可得 (cosα﹣sinα)2= ![]() .再由α是第二象限角,cosα﹣sinα<0,從而求得cosα﹣sinα 的值.
.再由α是第二象限角,cosα﹣sinα<0,從而求得cosα﹣sinα 的值.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數f(x)=Asin(ωx+φ)+B,A>0,ω>0,|φ|< ![]() 在某一個周期的圖象時,列表并填入了部分數據,如表:
在某一個周期的圖象時,列表并填入了部分數據,如表:
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin(ωx+φ)+B | 0 |
| 0 | ﹣ | 0 |
(1)請求出上表中的x1 , x2 , x3 , 并直接寫出函數f(x)的解析式;
(2)若3sin2 ![]() ﹣
﹣ ![]() mf(
mf( ![]() ﹣
﹣ ![]() )≥m+2對任意x∈[0,2π]恒成立,求實數m的取值范圍.
)≥m+2對任意x∈[0,2π]恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑,如圖,網格紙上正方形小格的邊長為1,圖中粗線畫出的是某幾何體毛坯的三視圖,第一次切削,將該毛坯得到一個表面積最大的長方體,第二次切削沿長方體的對角面刨開,得到兩個三棱柱,第三次切削將兩個三棱柱分別沿棱和表面的對角線刨開得到兩個鱉臑和兩個陽馬,則陽馬與鱉臑的體積之比為( ) 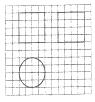
A.3:1
B.2:1
C.1:1
D.1:2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的公比q>1,且a1+a3=20,a2=8. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)設 ![]() ,Sn是數列{bn}的前n項和,對任意正整數n不等式
,Sn是數列{bn}的前n項和,對任意正整數n不等式 ![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解小學生的體能情況,抽取了某小學同年級部分學生進行跳繩測試,將所得數據整理后,畫出頻率分布直方圖如圖所示,已知圖中從左到右前三個小組的頻率分別是0.1,0.3,0.4,第一小組的頻數為5. 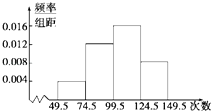
(1)求第四小組的頻率;
(2)參加這次測試的學生人數是多少?
(3)在這次測試中,學生跳繩次數的中位數落在第幾小組內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐P﹣ABCD中,底面ABCD為直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,則PB與平面PCD所成角的正弦值為( ) 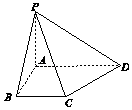
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐P﹣ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD為直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.點E在棱PA上,且PE=2EA. (Ⅰ)求異面直線PA與CD所成的角;
(Ⅱ)求證:PC∥平面EBD;
(Ⅲ)求二面角A﹣BE﹣D的大小.(用反三角函數表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面為直角梯形, ∠CDA=∠BAD=90°, ![]() ,M,N分別是PD,PB的中點.
,M,N分別是PD,PB的中點.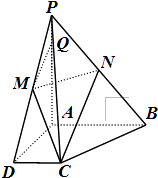
(1)求證:MQ∥平面PCB;
(2)求截面MCN與底面ABCD所成二面角的大小;
(3)求點A到平面MCN的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com