
【題目】足球運動被譽為“世界第一運動”.為推廣足球運動,某學校成立了足球社團由于報名人數較多,需對報名者進行“點球測試”來決定是否錄取,規則如下:
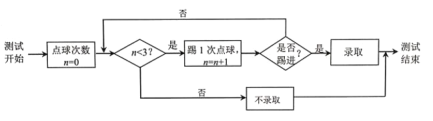
(1)下表是某同學6次的訓練數據,以這150個點球中的進球頻率代表其單次點球踢進的概率.為加入足球社團,該同學進行了“點球測試”,每次點球是否踢進相互獨立,將他在測試中所踢的點球次數記為![]() ,求
,求![]() ;
;
![]()
(2)社團中的甲、乙、丙三名成員將進行傳球訓練,從甲開始隨機地將球傳給其他兩人中的任意一人,接球者再隨機地將球傳給其他兩人中的任意一人,如此不停地傳下去,且假定每次傳球都能被接到.記開始傳球的人為第1次觸球者,接到第n次傳球的人即為第![]() 次觸球者
次觸球者![]() ,第n次觸球者是甲的概率記為
,第n次觸球者是甲的概率記為![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接寫出結果即可);
(直接寫出結果即可);
(ii)證明:數列![]() 為等比數列.
為等比數列.
【答案】(1)![]() (2)(i)
(2)(i)![]() ,
,![]() ,
,![]() (ii)證明見解析;
(ii)證明見解析;
【解析】
(1)先求出踢一次點球命中的概率,然后根據相互獨立事件的乘法公式分別求出![]() 取1,2,3的概率,再根據離散型隨機變量的期望公式可求得結果;
取1,2,3的概率,再根據離散型隨機變量的期望公式可求得結果;
(2)(i)根據傳球順序分析可得答案;(ii)根據題意可得![]() ,再變形為
,再變形為![]() ,根據等比數列的定義可證結論.
,根據等比數列的定義可證結論.
(1)這150個點球中的進球頻率為![]() ,
,
則該同學踢一次點球命中的概率![]() ,
,
由題意,![]() 可能取1,2,3,則
可能取1,2,3,則
![]() ,
,![]() ,
,![]() ,
,
則![]() 的期望
的期望![]() .
.
(2)(i)因為從甲開始隨機地將球傳給其他兩人中的任意一人,所以第1次觸球者是甲的概率![]() ,顯然第2次觸球者是甲的概率
,顯然第2次觸球者是甲的概率![]() ,第2次傳球有兩種可能,所以第3次觸球者是甲的概率概
,第2次傳球有兩種可能,所以第3次觸球者是甲的概率概![]() ,
,
(ii)∵第n次觸球者是甲的概率為![]() ,
,
所以當![]() 時,第
時,第![]() 次觸球者是甲的概率為
次觸球者是甲的概率為![]() ,第
,第![]() 次觸球者不是甲的概率為
次觸球者不是甲的概率為![]() ,
,
則![]() .
.
從而![]() ,又
,又![]() ,
,
∴![]() 是以
是以![]() 為首項,公比為
為首項,公比為![]() 的等比數列.
的等比數列.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
【題目】某城市有東西南北四個進入城區主干道的人口,在早高峰時間段,時常發生交通擁堵,交警部門記錄了11月份30天內的擁堵情況(如下表所示,其中●表示擁堵,○表示通暢).假設每個入口是否發生擁堵相互獨立,將各入口在這30天內擁堵的頻率代替各入口每天擁堵的概率.
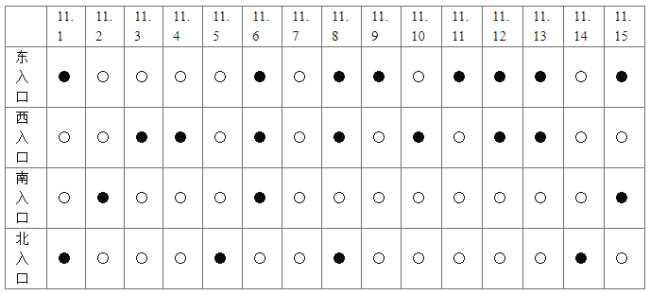
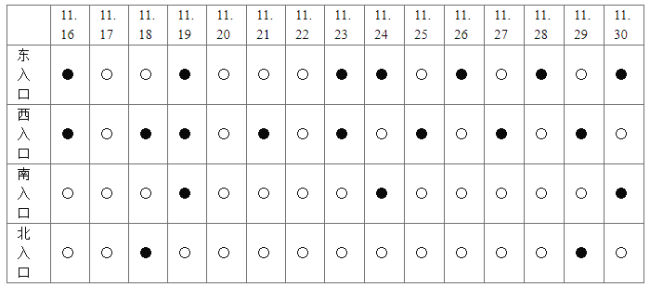
(1)分別求該城市一天中早高峰時間段這四個主干道的入口發生擁堵的概率.
(2)各入口一旦出現擁堵就需要交通協管員來疏通,聘請交通協管員有以下兩種方案可供選擇.方案一:四個主干道入口在早高峰時間段每天各聘請一位交通協管員,聘請每位交通協管員的日費用為m(![]() ,且
,且![]() )元.方案二:在早高峰時間段若某主干道入口發生擁堵,交警部門則需臨時調派兩位交通協管員協助疏通交通,調派后當日需給每位交通協管員的費用為200元.以四個主干道入口聘請交通協管員的日總費用的數學期望為依據,你認為在這兩個方案中應該如何選擇?請說明理由.
)元.方案二:在早高峰時間段若某主干道入口發生擁堵,交警部門則需臨時調派兩位交通協管員協助疏通交通,調派后當日需給每位交通協管員的費用為200元.以四個主干道入口聘請交通協管員的日總費用的數學期望為依據,你認為在這兩個方案中應該如何選擇?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽籺,俗稱“粽子”,古稱“角黍”,是端午節大家都會品嘗的食品,傳說這是為了紀念戰國時期楚國大臣、愛國主義詩人屈原.如圖,平行四邊形形狀的紙片是由六個邊長為![]() 的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球表面積的最大值為____.
的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球表面積的最大值為____.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 為正三角形,
為正三角形,![]() 是
是![]() 的中點,過
的中點,過![]() 的平面
的平面![]() 平行于平面
平行于平面![]() ,且平面
,且平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,與平面
,與平面![]() 的交線為
的交線為![]() .
.
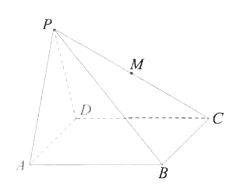
(1)在圖中作出四邊形![]() (不必說出作法和理由);
(不必說出作法和理由);
(2)若![]() ,四棱錐
,四棱錐![]() 的體積為
的體積為![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校同時提供![]() 、
、![]() 兩類線上選修課程,
兩類線上選修課程,![]() 類選修課每次觀看線上直播
類選修課每次觀看線上直播![]() 分鐘,并完成課后作業
分鐘,并完成課后作業![]() 分鐘,可獲得積分
分鐘,可獲得積分![]() 分;
分;![]() 類選修課每次觀看線上直播
類選修課每次觀看線上直播![]() 分鐘,并完成課后作業
分鐘,并完成課后作業![]() 分鐘,可獲得積分
分鐘,可獲得積分![]() 分.每周開設
分.每周開設![]() 次,共開設
次,共開設![]() 周,每次均為獨立內容,每次只能選擇
周,每次均為獨立內容,每次只能選擇![]() 類、
類、![]() 類課程中的一類學習.當選擇
類課程中的一類學習.當選擇![]() 類課程
類課程![]() 次,
次,![]() 類課程
類課程![]() 次時,可獲得總積分共_______分.如果規定學生觀看直播總時間不得少于
次時,可獲得總積分共_______分.如果規定學生觀看直播總時間不得少于![]() 分鐘,課后作業總時間不得少于
分鐘,課后作業總時間不得少于![]() 分鐘,則通過線上選修課的學習,最多可以獲得總積分共________分.
分鐘,則通過線上選修課的學習,最多可以獲得總積分共________分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法,如圖所示的程序框圖,給出了利用秦九韶算法求某多項式值的一個實例,若輸入x的值為2,則輸出![]() 的值為( )
的值為( )
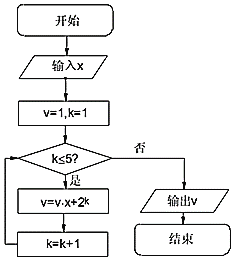
A.80B.192C.448D.36
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閏月年指農歷里有閏月的年份,比如2020年是閏月年,4月23日至5月22日為農歷四月,5月23日至6月20日為農歷閏四月.農歷置閏月是為了農歷年的平均長度接近回歸年:農歷年中的朔望月的平均長度為29.5306日,![]() 日,回歸年的總長度為365.2422日,兩者相差10.875日.因此,每19年相差206.625日,約等于7個朔望月.這樣每19年就有7個閏月年.以下是1640年至1694年間所有的閏月年:
日,回歸年的總長度為365.2422日,兩者相差10.875日.因此,每19年相差206.625日,約等于7個朔望月.這樣每19年就有7個閏月年.以下是1640年至1694年間所有的閏月年:
1640 | 1642 | 1645 | 1648 | 1651 | 1653 | 1656 |
1659 | 1661 | 1664 | 1667 | 1670 | 1672 | 1675 |
1678 | 1680 | 1 683 | 1686 | 1689 | 1691 | 1694 |
則從2020年至2049年,這30年間閏月年的個數為( )
A.10B.11C.12D.13
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com