
 的最小值.
的最小值.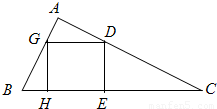
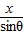 ,AC=atanθ,x,即可求出三角形ABC的面積f(θ)與正方形面積g(θ);
,AC=atanθ,x,即可求出三角形ABC的面積f(θ)與正方形面積g(θ); 的表達式,利用基本不等式,求出比值的最小值即可.
的表達式,利用基本不等式,求出比值的最小值即可. a2tanθ(0<θ<
a2tanθ(0<θ< )
)  ,由幾何關系知:∠AGD=θ
,由幾何關系知:∠AGD=θ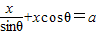 ⇒x=
⇒x=
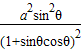 (0<θ<
(0<θ<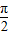 )
)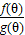 =
=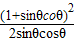 =1+
=1+ +
+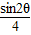 令:t=sin2θ
令:t=sin2θ
 =1+
=1+ (t+
(t+ )∵函數y=1+
)∵函數y=1+ (t+
(t+ )在(0,1]遞減
)在(0,1]遞減 (當且僅當t=1即θ=
(當且僅當t=1即θ=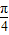 時成立)
時成立) 時,
時, 的最小值為
的最小值為 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
 22、如圖所示,在Rt△ABCD中,∠ACB=90°,點O為三角形外的一點,以O為圓心,OC為半徑的圓與邊AB相切,切點為E,圓O與邊BC相交于D點,直徑EF與邊BC交于G點,連接AC.
22、如圖所示,在Rt△ABCD中,∠ACB=90°,點O為三角形外的一點,以O為圓心,OC為半徑的圓與邊AB相切,切點為E,圓O與邊BC相交于D點,直徑EF與邊BC交于G點,連接AC.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,在Rt△ABC內有一內接正方形,它的一條邊在斜邊BC上,設AB=a,∠ABC=θ
如圖所示,在Rt△ABC內有一內接正方形,它的一條邊在斜邊BC上,設AB=a,∠ABC=θ| f(θ) | g(θ) |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
如圖所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| f(θ) |
| g(θ) |

查看答案和解析>>
科目:高中數學 來源:2009-2010學年東北三校高三第三次聯考數學試卷(理科)(解析版) 題型:解答題
 如圖所示,在Rt△ABCD中,∠ACB=90°,點O為三角形外的一點,以O為圓心,OC為半徑的圓與邊AB相切,切點為E,圓O與邊BC相交于D點,直徑EF與邊BC交于G點,連接AC.
如圖所示,在Rt△ABCD中,∠ACB=90°,點O為三角形外的一點,以O為圓心,OC為半徑的圓與邊AB相切,切點為E,圓O與邊BC相交于D點,直徑EF與邊BC交于G點,連接AC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com