
【題目】在三棱柱ABC﹣A1B1C1中,E是棱AB的中點,動點F是側面ACC1A1(包括邊界)上一點,若EF//平面BCC1B1,則動點F的軌跡是( )
A.線段B.圓弧
C.橢圓的一部分D.拋物線的一部分
【答案】A
【解析】
分別取AC,A1C1,A1B1的中點N,F,M,連接ME,MF,NE,EF,證明N,E,M,F共面,利用線面平行證明EF∥平面BCC1B1,則軌跡可求
如圖所示:
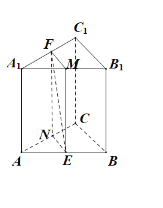
分別取AC,A1C1,A1B1的中點N,F,M,連接ME,MF,NE,EF,
因為E為AB的中點,所以NE∥BC且NE![]() ,FM∥B1C1,MF
,FM∥B1C1,MF![]() B1C1,
B1C1,
所以N,E,M,F共面,
所以ME∥BB1,NE∥BC,
所以ME∥平面BCC1B1,NE∥平面BCC1B1
而NE∩ME=E,BC∩BB1=B,
所以面NEMF∥平面BCC1B1,而EF![]() 面MN,
面MN,
所以EF∥平面BCC1B1,
所以要使EF∥平面BCC1B1,則動點F的軌跡為線段FN.
故選:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為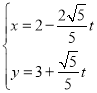 (
(![]() 為參數).
為參數).
(Ⅰ)求曲線![]() 的參數方程與直線
的參數方程與直線![]() 的普通方程;
的普通方程;
(Ⅱ)設點![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 和點
和點![]() 為直線
為直線![]() 上的點,且
上的點,且![]() .求
.求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,左右頂點分別為
,左右頂點分別為![]() ,
,![]() ,上頂點為
,上頂點為![]() ,
,![]()
(1)求橢圓離心率;
(2)點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求橢圓方程;
,求橢圓方程;
(3)在(2)的條件下,點![]() 在橢圓上且異于
在橢圓上且異于![]() 、
、![]() 兩點,直線
兩點,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,說明
,說明![]() 運動時以
運動時以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 的位置關系,并證明.
的位置關系,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面BB1C1C為菱形,![]() .
.
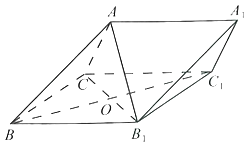
(1)求證:B1C⊥AB;
(2)若∠CBB1=60°,AC=BC,且點A在側面BB1C1C上的投影為點O,求二面角B﹣AA1﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年是我國垃圾分類逐步凸顯效果關鍵的一年.在國家高度重視,重拳出擊的前提下,高強度、高頻率的宣傳教育能有效縮短我國生活垃圾分類走入世界前列所需的時間,打好垃圾分類這場“持久戰”,“全民戰”.某市做了一項調查,在一所城市中學和一所縣城中學隨機各抽取15名學生,對垃圾分類知識進行問答,滿分為100分,他們所得成績如下:
城市中學學生成績分別為:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
縣城中學學生成績分別為:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根據上述兩組數據在圖中完成兩所中學學生成績的莖葉圖,并通過莖葉圖比較兩所中學學生成績的平均分及分散程度;(不要求計算出具體值,給出結論即可)
(2)從城市中學成績在80分以上的學生中抽取4名,記這4名學生的成績在90分以上的人數為X,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人經營淡水池塘養草魚,根據過去![]() 期的養殖檔案,該池塘的養殖重量
期的養殖檔案,該池塘的養殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的有
百斤的有![]() 期,不低于
期,不低于![]() 百斤且不超過
百斤且不超過![]() 百斤的有
百斤的有![]() 期,超過
期,超過![]() 百斤的有
百斤的有![]() 期.根據統計,該池塘的草魚重量的增加量
期.根據統計,該池塘的草魚重量的增加量![]() (百斤)與使用某種餌料的質量
(百斤)與使用某種餌料的質量![]() (百斤)之間的關系如圖所示.
(百斤)之間的關系如圖所示.
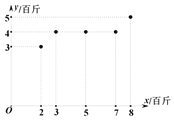
(1)根據數據可知![]() 與
與![]() 具有線性相關關系,請建立
具有線性相關關系,請建立![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;如果此人設想使用某種餌料
;如果此人設想使用某種餌料![]() 百斤時,草魚重量的增加量須多于
百斤時,草魚重量的增加量須多于![]() 百斤,請根據回歸方程計算,確定此方案是否可行?并說明理由.
百斤,請根據回歸方程計算,確定此方案是否可行?并說明理由.
(2)養魚的池塘對水質含氧量與新鮮度要求較高,某商家為該養殖戶提供收費服務,即提供不超過![]() 臺增氧沖水機,每期養殖使用的沖水機運行臺數與魚塘的魚重量
臺增氧沖水機,每期養殖使用的沖水機運行臺數與魚塘的魚重量![]() 有如下關系:
有如下關系:
魚的重量(單位:百斤) |
|
|
|
沖水機只需運行臺數 |
|
|
|
若某臺增氧沖水機運行,則商家每期可獲利![]() 千元;若某臺沖水機未運行,則商家每期虧損
千元;若某臺沖水機未運行,則商家每期虧損![]() 千元.視頻率為概率,商家欲使每期沖水機總利潤的均值達到最大,應提供幾臺增氧沖水機?
千元.視頻率為概率,商家欲使每期沖水機總利潤的均值達到最大,應提供幾臺增氧沖水機?
附:對于一組數據![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計公式分別為
的斜率和截距的最小二乘估計公式分別為
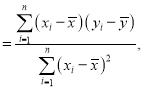
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com