已知函數,f(X)=log2x的反函數為f-1(x),等比數列{an}的公比為2,若f-1(a2)•f-1(a4)=210,則2f(a1)+f(a2)+…+f(a2009)=( )
A.21004×2008
B.21005×2009
C.21005×2008
D.21004×2009
【答案】
分析:本題由函數f(X)=log
2x可確定反函數f
-1(x),從而利用f
-1(a
2)•f
-1(a
4)=2
10得到等比數列第二項與第四項的等式關系,并結合公比為2求出通項a
n=2
n-1,由此求出
f(a1)+f(a2)+…+f(a2009)的值,進而可得答案.
解答:解:由f(X)=log
2x得f
-1(x)=2
x,所以f
-1(a
2)•f
-1(a
4)=
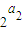
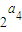
=
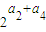
=2
10,所以a
2+a
4=10,
又公比q=2,所以a
1=1,
故a
n=2
n-1,
所以
f(a1)+f(a2)+…+f(a2009)=log
21+log
22
1+log
22
2+log
22
3+
…+log
22
2008=1+2+3+
…+2008=
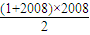
=1004×2009;
所以2
f(a1)+f(a2)+…+f(a2009)=21004×2009故選D.
點評:本題主要結合反函數知識考查了對數函數的運算性質,并兼顧了對等比數列知識的考查,綜合性較強,有一定難度,易在計算中出現失誤.

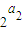
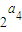 =
=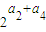 =210,所以a2+a4=10,
=210,所以a2+a4=10,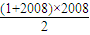 =1004×2009;
=1004×2009;

