
【題目】在某批次的某種燈泡中,隨機地抽取![]() 個樣品,并對其壽命進行追蹤調查,將結果列成頻率分布表如下.根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于
個樣品,并對其壽命進行追蹤調查,將結果列成頻率分布表如下.根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于![]() 天的燈泡是優等品,壽命小于
天的燈泡是優等品,壽命小于![]() 天的燈泡是次品,其余的燈泡是正品.
天的燈泡是次品,其余的燈泡是正品.
壽命(天) | 頻數 | 頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
|
(1)根據頻率分布表中的數據,寫出![]() 、
、![]() 的值;
的值;
(2)某人從燈泡樣品中隨機地購買了![]() 個,如果這
個,如果這![]() 個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求
個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求![]() 的最小值;
的最小值;
(3)某人從這個批次的燈泡中隨機地購買了![]() 個進行使用,若以上述頻率作為概率,用
個進行使用,若以上述頻率作為概率,用![]() 表示此人所購買的燈泡中次品的個數,求
表示此人所購買的燈泡中次品的個數,求![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)分布列見解析,
;(3)分布列見解析,![]() .
.
【解析】
(1)根據頻數、頻率和樣本容量之間的關系可得出![]() 、
、![]() 的值;
的值;
(2)由頻率分布表知按分層抽樣法,購買燈泡數![]() 個,由此能求出
個,由此能求出![]() 的最小值;
的最小值;
(3)![]() 的所有取值為
的所有取值為![]() 、
、![]() 、
、![]() 、
、![]() ,分別求出相對應的概率,由此能求出
,分別求出相對應的概率,由此能求出![]() 的分布列和數學期望.
的分布列和數學期望.
(1)由題意可得![]() ,
,![]() ;
;
(2)由表可知:燈泡樣品中優等品有![]() 個,正品有
個,正品有![]() 個,次品有
個,次品有![]() 個,
個,
![]() 優等品、正品和次品的比例為
優等品、正品和次品的比例為![]() ,
,
![]() 按分層抽樣法,購買燈泡數為
按分層抽樣法,購買燈泡數為![]() 個,
個,
因此,![]() 的最小值為
的最小值為![]() ;
;
(3)![]() 的所有取值為
的所有取值為![]() 、
、![]() 、
、![]() 、
、![]() ,
,
由題意,購買一個燈泡,且這個燈泡是次品的概率為![]() ,
,
從本批次燈泡中購買![]() 個,可看成
個,可看成![]() 次獨立重復試驗,則
次獨立重復試驗,則![]() .
.
![]() ,
,![]() ,
,
![]() ,
, .
.
所以,隨機變量![]() 的分布列如下表所示:
的分布列如下表所示:
|
|
|
|
|
|
|
|
|
|
因此,隨機變量![]() 的數學期望為
的數學期望為![]() .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程是 (φ為參數,a>0),直線l的參數方程是
(φ為參數,a>0),直線l的參數方程是![]() (t為參數),曲線C與直線l有一個公共點在x軸上,以坐標原點為極點,x軸的正半軸為極軸建立坐標系.
(t為參數),曲線C與直線l有一個公共點在x軸上,以坐標原點為極點,x軸的正半軸為極軸建立坐標系.
(1)求曲線C的普通方程;
(2)若點A(ρ1,θ),B(ρ2,θ+![]() ),C(ρ3,θ+
),C(ρ3,θ+![]() )在曲線C上,求
)在曲線C上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 已知函數f(x)=|x+a|+|x-2|.
(1)當a=-3時,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列的定義為:在一個數列中,從第二項起,如果每一項與它的前一項的差都為同一個常數,那么這個數叫做等差數列,這個常數叫做該數列的公差.類比等差數列的定義給出“等和數列”的定義:_____________________________________;已知數列![]() 是等和數列,且
是等和數列,且![]() ,公和為
,公和為![]() ,那么
,那么![]() 的值為____________.這個數列的前
的值為____________.這個數列的前![]() 項和
項和![]() 的計算公式為_____________________________________.
的計算公式為_____________________________________.
查看答案和解析>>
科目:高中數學 來源: 題型:
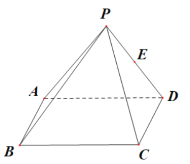
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() ,側面
,側面![]() 為等邊三角形且垂直于底面
為等邊三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)在棱![]() 上取一點
上取一點![]() 使直線
使直線![]() ∥平面
∥平面![]() 并證明;
并證明;
(2)在(1)的條件下,當棱![]() 上存在一點
上存在一點![]() ,使得直線
,使得直線![]() 與底面
與底面![]() 所成角為
所成角為![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 為1,2,3,…,
為1,2,3,…,![]() 的一個排列,若
的一個排列,若![]() 互不相同,則稱數列
互不相同,則稱數列![]() 具有性質
具有性質![]() .
.
(1)若![]() ,且
,且![]() ,寫出具有性質
,寫出具有性質![]() 的所有數列
的所有數列![]() ;
;
(2)若數列![]() 具有性質
具有性質![]() ,證明:
,證明:![]() ;
;
(3)當![]() 時,分別判斷是否存在具有性質
時,分別判斷是否存在具有性質![]() 的數列
的數列![]() ?請說明理由.
?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校高三年級共1000名男生中隨機抽取50人測量身高,據測量,被測學生身高全部介于![]() 到
到![]() 之間,將測量結果按如下方式分成八組:第一組
之間,將測量結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() .如圖是按上述分組方法得到的頻率分布直方圖的一部分.其中第六組、第七組、第八組人數依次構成等差數列.
.如圖是按上述分組方法得到的頻率分布直方圖的一部分.其中第六組、第七組、第八組人數依次構成等差數列.
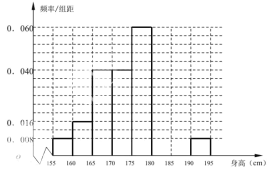
(1)求第六組、第七組的頻率,并估計高三年級全體男生身高在![]() 以上(含
以上(含![]() )的人數;
)的人數;
(2)學校決定讓這五十人在運動會上組成一個高旗隊,在這五十人中要選身高在![]() 以上(含
以上(含![]() )的兩人作為隊長,求這兩人在同一組的概率.
)的兩人作為隊長,求這兩人在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了解本市1萬名小學生的普通話水平,在全市范圍內進行了普通話測試,測試后對每個小學生的普通話測試成績進行統計,發現總體(這1萬名小學生普通話測試成績)服從正態分布![]() .
.
(1)從這1萬名小學生中任意抽取1名小學生,求這名小學生的普通話測試成績在![]() 內的概率;
內的概率;
(2)現在從總體中隨機抽取12名小學生的普通話測試成績,對應的數據如下:50,52,56,62,63,68,65,64,72,80,67,90.從這12個數據中隨機選取4個,記![]() 表示大于總體平均分的個數,求
表示大于總體平均分的個數,求![]() 的方差.
的方差.
參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com