【題目】設函數
，
.
（1）當
（
為自然對數的底數）時，求
的極小值；
（2）討論函數
零點的個數.
【答案】（1）極小值
；
（2）①當
時，
無零點，
②當
或
時，有且僅有
個零點，
③當
時，有兩個零點.
【解析】
試題（1）要求
的極小值，可以通過判斷其單調性從而求得其極小值，對求導，可知
，再通過列表即可得當
時，
取得極小值
；（2）令
，可得
，因此要判斷函數
的零點個數，可通過畫出函數
的草圖來判斷，同樣可以通過求導判斷函數的單調性來畫出函數圖象的草圖：
，通過列表可得到
的單調性，作出
的圖象，進而可得
①當
時，
無零點，②當或
時，有且僅有個零點，
③當
時，有兩個零點.
試題解析：（1）當
時，
，其定義域為
，
，
令
，，
|
|
|
|
|
|
|
|
|
| 極小值 |
|
故當時，取得極小值；
（2）
，其定義域為，
令
，得，
設
，其定義域為.則的零點為與
的交點，
，
|
|
|
|
|
|
|
|
|
| 極大值 |
|
故當
時，取得最大值
作出的圖象，可得
①當時，無零點，
②當或時，有且僅有個零點，
③當時，有兩個零點.
科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是（ ）
A.命題“若
，則
”的逆否命題是“若
，則
”
B.“
”是“
”的充分不必要條件
C.若
為假命題，則
、
均為假命題
D.命題：“
，使得
”，則非：“
，
”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個正方形花圃被分成5份．
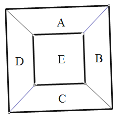
（1）若給這5個部分種植花，要求相鄰兩部分種植不同顏色的花，己知現有紅、黃、藍、綠4種顏色不同的花，求有多少種不同的種植方法?
（2）若將6個不同的盆栽都擺放入這5個部分，且要求每個部分至少有一個盆栽，問有多少種不同的放法?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列判斷正確的是（ ）
A.若隨機變量
服從正態分布
，
，則
；
B.已知直線
平面
，直線
平面
，則“
”是“
”的必要不充分條件；
C.若隨機變量服從二項分布：
，則
；
D.已知直線
經過點
，則
的取值范圍是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在2018年俄羅斯世界杯期間,莫斯科的部分餐廳經營了來自中國的小龍蝦,這些小龍蝦標有等級代碼.為得到小龍蝦等級代碼數值
與銷售單價
之間的關系,經統計得到如下數據：
等級代碼數值 | 38 | 48 | 58 | 68 | 78 | 88 |
銷售單價 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知銷售單價與等級代碼數值之間存在線性相關關系,求關于的線性回歸方程(系數精確到0.1)；
（2）若莫斯科某餐廳銷售的中國小龍蝦的等級代碼數值為98，請估計該等級的中國小龍蝦銷售單價為多少元？
參考公式：對一組數據
,
，····
,其回歸直線
的斜率和截距最小二乘估計分別為：
,
.
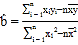參考數據：
,
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小型企業甲產品生產的投入成本x（單位：萬元）與產品銷售收入y（單位：萬元）存在較好的線性關系，下表記錄了最近5次該產品的相關數據.
x（萬元） | 3 | 5 | 7 | 9 | 11 |
y（萬元） | 8 | 10 | 13 | 17 | 22 |
（1）求y關于x的線性回歸方程；
（2）根據（1）中的回歸方程，判斷該企業甲產品投入成本12萬元的毛利率更大還是投入成本15萬元的毛利率更大（毛利率
）？
相關公式：
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）
已知函數
是奇函數，的定義域為
．當
時， 
．(e為自然對數的底數)．
(1)若函數在區間
上存在極值點，求實數
的取值范圍；
(2)如果當x≥1時，不等式
恒成立，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法：
①對于獨立性檢驗，
的值越大，說明兩事件相關程度越大；
②以模型
去擬合一組數據時，為了求出回歸方程，設
，將其變換后得到線性方程
，則
，
的值分別是
和0.3；
③已知隨機變量
，若
，則
（
）的值為
；
④通過回歸直線
及回歸系數
，可以精確反映變量的取值和變化趨勢．
其中錯誤的選項是（ ）
A.①B.②C.③D.④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
