【題目】如圖， 
表示神風摩托車廠一天的銷售收入與摩托車銷售量的關系； 
表示摩托車廠一天的銷售成本與銷售量的關系．
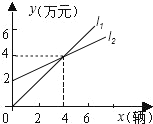
（1）寫出銷售收入與銷售量之間的函數關系式；
（2）寫出銷售成本與銷售量之間的函數關系式；
（3）當一天的銷售量為多少輛時，銷售收入等于銷售成本；
（4）當一天的銷售超過多少輛時，工廠才能獲利？（利潤=收入-成本）
七星圖書口算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】已知點
為圓
的圓心， 
是圓上動點，點
在圓的半徑
上，且有點
和
上的點
，滿足
（1）當
在圓上運動時，求點
的軌跡方程；
（2）若斜率為
的直線
與圓
相切，與（1）中所求點
的軌跡教育不同的兩點
是坐標原點，且
時，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過點
的直線與圓
相切，且與直線
垂直，則
（ ）
A. 2 B. 1 C. 
D. 
【答案】A
【解析】因為點P(2,2)滿足圓
的方程，所以P在圓上，
又過點P(2,2)的直線與圓
相切，且與直線axy+1=0垂直，
所以切點與圓心連線與直線axy+1=0平行，
所以直線axy+1=0的斜率為： 
.
故選A.
點睛：對于直線和圓的位置關系的問題，可用“代數法”或“幾何法”求解，直線與圓的位置關系體現了圓的幾何性質和代數方法的結合，“代數法”與“幾何法”是從不同的方面和思路來判斷的，解題時不要單純依靠代數計算，若選用幾何法可使得解題過程既簡單又不容易出錯．
【題型】單選題
【結束】
23
【題目】設
分別是雙曲線
的左、右焦點.若點
在雙曲線上，且
，則
（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高二年級進行了百科知識大賽，為了了解高二年級900名同學的比賽情況，現在甲、乙兩個班級各隨機抽取了10名同學的成績，比賽成績滿分為100分，80分以上可獲得二等獎，90分以上可以獲得一等獎，已知抽取的兩個班學生的成績（單位：分）數據的莖葉圖如圖1所示:
（1）比較兩組數據的分散程度（只需要給出結論），并求出甲組數據的頻率分布直方圖如圖2中所示的
值；
（2）現從兩組數據中獲獎的學生里分別隨機抽取一人接受采訪，求被抽中的甲班學生成績高于乙班學生成績的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校射擊隊的某一選手射擊一次，其命中環數的概率如表：
命中環數 | 10環 | 9環 | 8環 | 7環 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該選手射擊一次，
(1)命中9環或10環的概率.
(2)至少命中8環的概率.
(3)命中不足8環的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
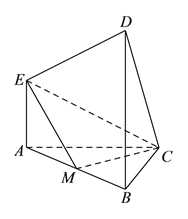
【題目】在如圖所示的多面體中， 
平面
， 
平面
， 
，且
， 
是
的中點．
（Ⅰ）求證： 
．
（Ⅱ）求平面
與平面
所成的銳二面角的余弦值．
（Ⅲ）在棱
上是否存在一點
，使得直線
與平面
所成的角是
．若存在，指出點
的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
過兩點
， 
，且圓心
在直線
上．
（Ⅰ）求圓
的標準方程；
（Ⅱ）直線
過點
且與圓
有兩個不同的交點
， 
，若直線
的斜率
大于0，求
的取值范圍；
（Ⅲ）在（Ⅱ）的條件下，是否存在直線
使得弦
的垂直平分線過點
，若存在，求出直線
的方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f(x)＝a(x－5)2＋6lnx，其中a∈R，曲線y＝f(x)在點(1，f(1))處的切線與y軸相交于點(0,6)．
(1)確定a的值；
(2)求函數f(x)的單調區間與極值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
