
【題目】已知![]() (
(![]() ).
).
(Ⅰ)判斷當![]() 時
時![]() 的單調性;
的單調性;
(Ⅱ)若![]() ,
,![]() (
(![]() )為
)為![]() 兩個極值點,求證:
兩個極值點,求證:![]() .
.
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數),以平面直角坐標系的原點
為參數),以平面直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,將曲線
軸的非負半軸為極軸建立極坐標系,將曲線![]() 繞極點順時針旋轉
繞極點順時針旋轉![]() 后得到曲線的曲線記為
后得到曲線的曲線記為![]() .
.
(1)求曲線![]() 和
和![]() 的極坐標方程;
的極坐標方程;
(2)設![]() 和
和![]() 的交點為
的交點為![]() ,
,![]() ,求
,求![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代著名數學家劉徽的杰作《九章算術注》是中國最寶貴的數學遺產之一,書中記載了他計算圓周率所用的方法.先作一個半徑為1的單位圓,然后做其內接正六邊形,在此基礎上做出內接正![]() 邊形,這樣正多邊形的邊逐漸逼近圓周,從而得到圓周率,這種方法稱為“劉徽割圓術”.現設單位圓
邊形,這樣正多邊形的邊逐漸逼近圓周,從而得到圓周率,這種方法稱為“劉徽割圓術”.現設單位圓![]() 的內接正
的內接正![]() 邊形的一邊為
邊形的一邊為![]() ,點
,點![]() 為劣弧
為劣弧![]() 的中點,則
的中點,則![]() 是內接正
是內接正![]() 邊形的一邊,現記
邊形的一邊,現記![]() ,
,![]() ,則( )
,則( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三(1)班在一次語文測試結束后,發現同學們在背誦內容方面失分較為嚴重.為了提升背誦效果,班主任倡議大家在早、晚讀時間站起來大聲誦讀,為了解同學們對站起來大聲誦讀的態度,對全班50名同學進行調查,將調查結果進行整理后制成下表:
考試分數 |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 5 | 10 | 5 |
贊成人數 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使測試優秀率為30%,則優秀分數線應定為多少分?
(2)依據第1問的結果及樣本數據研究是否贊成站起來大聲誦讀的態度與考試成績是否優秀的關系,列出2×2列聯表,并判斷是否有90%的把握認為贊成與否的態度與成績是否優秀有關系.
參考公式及數據: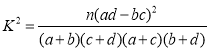 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于某種類型的口服藥,口服![]() 小時后,由消化系統進入血液中藥物濃度
小時后,由消化系統進入血液中藥物濃度![]() (單位)與時間
(單位)與時間![]() 小時的關系為
小時的關系為![]() ,其中
,其中![]() ,
,![]() 為常數,對于某一種藥物
為常數,對于某一種藥物![]() ,
,![]() ,
,![]() .
.
(1)口服藥物后______小時血液中藥物濃度最高;
(2)這種藥物服藥![]() 小時后血液中藥物濃度如下表
小時后血液中藥物濃度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一個病人上午8:00第一次服藥,要使得病人血液中藥物濃度保持在0.5個單位以上,第三次服藥時間是______(時間以整點為準)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】筆、墨、紙、硯是中國獨有的文書工具,即文房四寶.筆、墨、紙、硯之名,起源于南北朝時期,其中“紙”指的是宣紙,“始于唐代,產于涇縣”,因唐代涇縣隸屬宣州管轄,故因地得名宣紙,宣紙按質量等級分類可分為正牌和副牌(優等品和合格品)某公司生產的宣紙為純手工制作,年產宣紙10000刀,該公司按照某種質量指標x給宣紙確定質量等級,如下表所示:
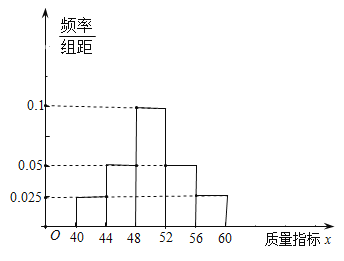
x的范圍 |
|
|
|
質量等級 | 正牌 | 副牌 | 廢品 |
公司在所生產的宣紙中隨機抽取了一刀(100張)進行檢驗,得到的頻率分布直方圖如上圖所示.已知每張正牌宣紙的利潤為12元,副牌宣紙的利潤為6元,廢品宣紙的利潤為-12元.
(1)試估計該公司生產宣紙的利潤;
(2)該公司預備購買一種售價為100萬元的機器改進生產工藝,這種機器使用壽命為一年,不影響產量,這種機器生產的宣紙的質量指標x服從正態分布![]() ,改進工藝后正牌和副牌宣紙的利潤都將受到不同程度的影響,觀測的數據如下表所示:
,改進工藝后正牌和副牌宣紙的利潤都將受到不同程度的影響,觀測的數據如下表所示:
x的范圍 |
|
| ||
一張宣紙的利潤 | 12 | 8 | 8 | 3 |
頻率 | 0.5 | 0.5 | 0.5 | 0.5 |
將頻率視為概率,請判斷該公司是否應該購買這種機器,并說明理由
附:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為進一步規范校園管理,強化飲食安全,提出了“遠離外賣,健康飲食”的口號.當然,也需要學校食堂能提供安全豐富的菜品來滿足同學們的需求.在學期末,校學生會為了調研學生對本校食堂A部和B部的用餐滿意度,從在A部和B部都用過餐的學生中隨機抽取了200人,每人分別對其評分,滿分為100分.隨后整理評分數據,將分數分成6組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,第6組
,第6組![]() ,得到A部分數的頻率分布直方圖和B部分數的頻數分布表.
,得到A部分數的頻率分布直方圖和B部分數的頻數分布表.

分數區間 | 頻數 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定義:學生對食堂的“滿意度指數”
分數 |
|
|
|
|
|
|
滿意度指數 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位數(精確到小數點后一位);
(2)A部為進一步改善經營,從打分在80分以下的前四組中,采用分層抽樣的方法抽取8人進行座談,再從這8人中隨機抽取3人參與“端午節包粽子”實踐活動,在第3組抽到1人的情況下,第4組抽到2人的概率;
(3)如果根據調研結果評選學生放心餐廳,應該評選A部還是B部(將頻率視為概率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,
,![]() ,記
,記![]() ,
,![]() ,若同時滿足條件①
,若同時滿足條件①![]() ,
,![]() 均單調遞增;②
均單調遞增;②![]() 且
且![]() ,則稱
,則稱![]() ,
,![]() 是無窮互補數列.
是無窮互補數列.
(1)若![]() ,
,![]() ,試判斷數列
,試判斷數列![]() ,
,![]() 是否為無窮互補數列,并說明理由;
是否為無窮互補數列,并說明理由;
(2)若![]() ,且
,且![]() ,
,![]() 是無窮互補數列,求數列
是無窮互補數列,求數列![]() 前
前![]() 項的和.
項的和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com