日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

（1）從1,2,3,4,5五個數中依次取2個數，求這兩個數的差的絕對值等于1的概率；

（2）△ABC中，∠B=60°，∠C=45°，高AD=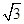，在BC邊上任取一點M，求 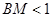的概率.

 

【答案】

（1） （2）

【解析】

試題分析：（1）根據題意，要使得從1,2,3,4,5五個數中依次取2個數，所有的情況有10種，而對于這兩個數的差的絕對值等于1有2，1；2，3；3，4；4，5；有4種，沒有順序，故可知概率值為   7分

（2）△ABC中，∠B=60°，∠C=45°，高AD=，在BC邊上任取一點M 的所有的可能值的長度為 2，而對于的概率即為   14分

考點：古典概型和幾何概型

點評：解決的關鍵是根據試驗的基本事件空間來分析事件的基本事件術，以及區域長度來求解概率，屬于基礎題。

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

為了比較兩種治療失眠癥的藥（分別成為A藥，B藥）的療效，隨機地選取20位患者服用A藥，20位患者服用B藥，這40位患者服用一段時間后，記錄他們日平均增加的睡眠時間（單位：h）實驗的觀測結果如下：
服用A藥的20位患者日平均增加的睡眠時間：
0.6   1.2   2.7   1.5    2.8   1.8   2.2   2.3    3.2   3.5
2.5   2.6   1.2   2.7    1.5   2.9   3.0   3.1    2.3   2.4
服用B藥的20位患者日平均增加的睡眠時間：
3.2    1.7     1.9     0.8     0.9    2.4     1.2     2.6     1.3     1.4
1.6    0.5     1.8     0.6     2.1    1.1     2.5     1.2     2.7     0.5
（Ⅰ）分別計算兩種藥的平均數，從計算結果看，哪種藥的療效更好？
（Ⅱ）根據兩組數據完成下面莖葉圖，從莖葉圖看，哪種藥的療效更好？

查看答案和解析>>

科目：高中數學 來源： 題型：

某日用品按行業質量標準分成五個等級，等級系數X依次為1,2,3,4,5．現從一批該日用品中隨機抽取20件，對其等級系數進行統計分析，得到頻率分布表如下：

X

1

2

3

4

5

頻率

a

0．2

0．45

b

c

（1）若所抽取的20件日用品中，等級系數為4的恰有3件，等級系數為5的恰有2件，求a，b，c的值；

  （2）在（1）的條件下，將等級系數為4的3件日用品記為x1，x2，x3，等級系數為5的2件日用品記為y1，y2，現從x1，x2，x3，y1，y2這5件日用品中任取兩件（假定每件日用品被取出的可能性相同），寫出所有可能的結果，并求這兩件日用品的等級系數恰好相等的概率．

查看答案和解析>>

科目：高中數學 來源：江西省重點中學盟校2011-2012學年高三第一次聯考（數學文） 題型：解答題

 

    某日用品按行業質量標準分成五個等級，等級系數X依次為1,2,3,4,5．現從一批該日用品中隨機抽取20件，對其等級系數進行統計分析，得到頻率分布表如下：

X

1

2

3

4

5

頻率

a

0．2

0．4

b

c

    （I）若所抽取的20件日用品中，等級系數為4的恰有3件，等級系數為5的恰有2件，求a，b，c的值；

    （Ⅱ）在（I）的條件下，將等級系數為4的3件日用品記為x1，x2，x3，等級系數為5的2件日用品記為y1，y2，現從x1，x2，x3，y1，y2這5件日用品中任取兩件（假定每件日用品被取出的可能性相同），寫出所有可能的結果，并求這兩件日用品的等級系數恰好相等的概率．

 

 

 

 

 

 

 

查看答案和解析>>

科目：高中數學 來源：2011-2012學年山東省高考模擬預測數學文試卷（解析版） 題型：解答題

一個袋中裝有四個形狀大小完全相同的球，球的編號分別為1，2，3，4．

（I）從袋中隨機抽取一個球，將其編號記為，然后從袋中余下的三個球中再隨機抽取一個球，將其編號記為．求關于的一元二次方程有實根的概率；

（II）先從袋中隨機取一個球，該球的編號為m，將球放回袋中，然后再從袋中隨機取一個球，該球的編號為n．若以 作為點P的坐標，求點P落在區域內的概率．

【解析】第一問利用古典概型概率求解所有的基本事件數共12種，然后利用方程有實根，則滿足△=4a2-4b2≥0，即a2≥b2。，這樣求得事件發生的基本事件數為6種，從而得到概率。第二問中，利用所有的基本事件數為16種。即基本事件（m，n）有：（1，1）  （1,2）   （1,3）  （1,4）   （2,1）  （2，2）  （2,3）   （2,4）   （3,1）   （3,2）  （3，3）    （3,4）   （4,1）   （4,2）   （4,3）  （4，4）共16種。在求解滿足的基本事件數為（1，1） （2,1）  （2，2） （3,1） 共4種，結合古典概型求解得到概率。

（1）基本事件（a，b）有：（1,2）   （1,3）  （1,4）   （2,1）   （2,3）   （2,4）   （3,1）   （3,2）  （3,4）   （4,1）   （4,2）   （4,3）共12種。

∵有實根， ∴△=4a2-4b2≥0，即a2≥b2。

記“有實根”為事件A，則A包含的事件有：（2,1）   （3,1）   （3,2）  （4,1）   （4,2）   （4,3） 共6種。

∴PA.= 。   …………………6分

（2）基本事件（m，n）有：（1，1）  （1,2）   （1,3）  （1,4）   （2,1）  （2，2）  （2,3）   （2,4）   （3,1）   （3,2）  （3，3）    （3,4）   （4,1）   （4,2）   （4,3）  （4，4）共16種。

記“點P落在區域內”為事件B，則B包含的事件有：

（1，1） （2,1）  （2，2） （3,1） 共4種。∴PB.=

 

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 特一级黄色片 | 一区二区不卡在线观看 | 国产色在线 | 久久精品视频免费观看 | 国产探花在线看 | 日韩一区二区在线播放 | 九九热这里只有精品6 | 国产成人一区二区三区 | 天堂成人国产精品一区 | 欧美日韩激情在线 | 欧美日韩在线观看视频 | 国产成人高清视频 | av电影中文字幕在线观看 | 91精品亚洲 | 国产91在线免费观看 | 日韩美女国产精品 | 蜜臀视频在线观看 | 精品 99| 6080亚洲精品一区二区 | 欧美日韩一区在线 | 日韩资源在线 | 欧美一级欧美三级在线观看 | 污视频网站入口 | 欧美在线视频一区 | 亚洲国产精品成人综合色在线婷婷 | 超碰在线看 | 成人国产一区二区 | 99在线国产 | 亚洲精美视频 | 国产视频网 | 日韩乱码中文字幕 | 欧美成人精品一区二区男人看 | 国产精品久久久久久影院8一贰佰 | 久久电影中文字幕 | 久久精品一区视频 | 久草视| 久久久久久国产 | 国产在线小视频 | 亚洲精品电影在线观看 | 黄色a在线观看 | 欧美成人手机在线视频 |