
【題目】已知函數![]() ,
,![]()
(1)求證![]() 在
在![]() 上遞增;
上遞增;
(2)若![]() 在
在![]() 上的值域是
上的值域是![]() ,求實數a的取值范圍;
,求實數a的取值范圍;
(3)當![]() 在
在![]() 上恒成立,求實數a的取值范圍.
上恒成立,求實數a的取值范圍.
科目:高中數學 來源: 題型:
【題目】某醫學院欲研究晝夜溫差大小與患感冒人數多少之間的關系,該協會分別到氣象局與某醫院抄錄了1到6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到數據資料見下表:

該院確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(Ⅰ)求選取的2組數據恰好是不相鄰的兩個月的概率;
(Ⅱ)已知選取的是1月與6月的兩組數據.
(1)請根據2到5月份的數據,求出就診人數![]() 關于晝夜溫差
關于晝夜溫差![]() 的線性回歸方程;
的線性回歸方程;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該協會所得線性回歸方程是否理想?
(參考公式和數據: 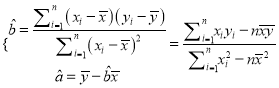
![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某籃球隊對籃球運動員的籃球技能進行統計研究,針對籃球運動員在投籃命中時,運動員在籃筐中心的水平距離這項指標,對某運動員進行了若干場次的統計,依據統計結果繪制如下頻率分
布直方圖:

(1)依據頻率分布直方圖估算該運動員投籃命中時,他到籃筐中心的水平距離的中位數;
(2)若從該運動員投籃命中時,他到籃筐中心的水平距離為2到5米的這三組中,用分層抽樣的方法抽取7次成績(單位:米,運動員投籃命中時,他到籃筐中心的水平距離越遠越好),并從抽到的這7次成績中隨機抽取2次.規定:這2次成績均來自到籃筐中心的水平距離為4到5米的這一組,記 1分,否則記0分.求該運動員得1分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() =2px(p>0)的準線方程為x=-
=2px(p>0)的準線方程為x=-![]() ,F為拋物線的焦點
,F為拋物線的焦點
(I)求拋物線C的方程;
(II)若P是拋物線C上一點,點A的坐標為(![]() ,2),求
,2),求![]() 的最小值;
的最小值;
(III)若過點F且斜率為1的直線與拋物線C交于M,N兩點,求線段MN的中點坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
極坐標系與直角坐標系![]() 有相同的長度單位,以坐標原點
有相同的長度單位,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸.已知曲線
軸正半軸為極軸.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,射線
,射線![]() 與曲線
與曲線![]() 分別交異于極點
分別交異于極點![]() 的四點
的四點![]() .
.
(1)若曲線![]() 關于曲線
關于曲線![]() 對稱,求
對稱,求![]() 的值,并把曲線
的值,并把曲線![]() 和
和![]() 化成直角坐標方程;
化成直角坐標方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,
的焦點,![]() 為拋物線
為拋物線![]() 上三點,且點
上三點,且點![]() 在第一象限,直線
在第一象限,直線![]() 經過點
經過點![]() 與拋物線
與拋物線![]() 在點
在點![]() 處的切線平行,點
處的切線平行,點![]() 為
為![]() 的中點.
的中點.
(1)證明:![]() 與
與![]() 軸平行;
軸平行;
(2)求![]() 面積
面積![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩種離子在小鼠體內的殘留程度,進行如下試驗:將200只小鼠隨機分成![]() 兩組,每組100只,其中
兩組,每組100只,其中![]() 組小鼠給服甲離子溶液,
組小鼠給服甲離子溶液,![]() 組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖:
組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖:

記![]() 為事件:“乙離子殘留在體內的百分比不低于
為事件:“乙離子殘留在體內的百分比不低于![]() ”,根據直方圖得到
”,根據直方圖得到![]() 的估計值為
的估計值為![]() .
.
(1)求乙離子殘留百分比直方圖中![]() 的值;
的值;
(2)分別估計甲、乙離子殘留百分比的平均值(同一組中的數據用該組區間的中點值為代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放以來,人們的支付方式發生了巨大轉變.近年來,移動支付已成為主要支付方式之一.為了解某校學生上個月A,B兩種移動支付方式的使用情況,從全校學生中隨機抽取了100人,發現樣本中A,B兩種支付方式都不使用的有5人,樣本中僅使用A和僅使用B的學生的支付金額分布情況如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
僅使用A | 18人 | 9人 | 3人 |
僅使用B | 10人 | 14人 | 1人 |
(Ⅰ)從全校學生中隨機抽取1人,估計該學生上個月A,B兩種支付方式都使用的概率;
(Ⅱ)從樣本僅使用A和僅使用B的學生中各隨機抽取1人,以X表示這2人中上個月支付金額大于1000元的人數,求X的分布列和數學期望;
(Ⅲ)已知上個月樣本學生的支付方式在本月沒有變化.現從樣本僅使用A的學生中,隨機抽查3人,發現他們本月的支付金額都大于2000元.根據抽查結果,能否認為樣本僅使用A的學生中本月支付金額大于2000元的人數有變化?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com