
【題目】已知△ABC,若存在△A1B1C1 , 滿足 ![]() =
= ![]() =
= ![]() =1,則稱△A1B1C1是△ABC的一個“友好”三角形.在滿足下述條件的三角形中,存在“友好”三角形的是:(請寫出符合要求的條件的序號) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
=1,則稱△A1B1C1是△ABC的一個“友好”三角形.在滿足下述條件的三角形中,存在“友好”三角形的是:(請寫出符合要求的條件的序號) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
【答案】②
【解析】解:①項,A=90°,cosA=0=sinA1 , A1=180°或0,不滿足三角形內角和為180°的條件,故①項不符合條件; ②項,cosC=cos45°=sinC1 , 則C1=45°或135°;cosB=cos60°= ![]() =sinB1 , 則B1=30°或150°,
=sinB1 , 則B1=30°或150°,
又三角形內角和為180°,
∴△A1B1C1可能的組合是: 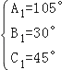 或
或 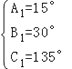 ,
,
第一種情況A1=105°時,cosA=cos75°≠sin105°,這種情況不符合題意;
當第二種情況A1=15°,滿足滿足cosA=cos75°=sin15°,故②項符合條件;
③項,cosC=cos30°=sinC1 , 則C1=60°或120°,又A=B=75°,
∴A1=B1 ,
當C1=60時,A1=B1=C1=60°,![]() ≠
≠ ![]() ,即
,即 ![]() ≠
≠ ![]() ,不符合題意;
,不符合題意;
當C1=120°時,A1=B1=30°,則 ![]() ≠
≠ ![]() ,即
,即 ![]() ≠
≠ ![]() ,故③項不符合條件;
,故③項不符合條件;
由A+B+C≠180°,不能構成三角形,故④項不符合條件;
所以答案是:②


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,底面ABCD是棱長為2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中點,若H為PD上的動點,EH與平面PAD所成最大角的正切值為 ![]() .
. 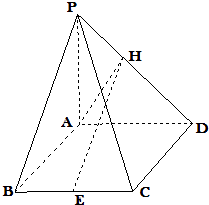
(1)當EH與平面PAD所成角的正切值為 ![]() 時,求證:EH∥平面PAB;
時,求證:EH∥平面PAB;
(2)在(1)的條件下,求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次歌手大獎賽上,七位評委為歌手打出的分數如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一個最高分和一個最低分后,所剩數據的平均值和方差分別為( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等比數列,且滿足a2+a5=36,a3a4=128. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)若數列{an}是遞增數列,且bn=an+log2an(n∈N*),求數列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉軸旋轉,有下列結論:
①當直線AB與a成60°角時,AB與b成30°角;
②當直線AB與a成60°角時,AB與b成60°角;
③直線AB與a所稱角的最小值為45°;
④直線AB與a所稱角的最小值為60°;
其中正確的是________。(填寫所有正確結論的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓![]() 的左、右焦點分別為F1,F2,離心率為
的左、右焦點分別為F1,F2,離心率為![]() ,兩準線之間的距離為8.點P在橢圓E上,且位于第一象限,過點F1作直線PF1的垂線l1,過點F2作直線PF2的垂線l2.
,兩準線之間的距離為8.點P在橢圓E上,且位于第一象限,過點F1作直線PF1的垂線l1,過點F2作直線PF2的垂線l2.
(1)求橢圓E的標準方程;
(2)若直線l1,l2的交點Q在橢圓E上,求點P的坐標.
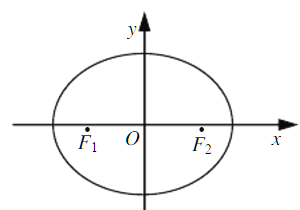
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過對某城市一天內單次租用共享自行車的時間![]() 分鐘到
分鐘到![]() 鐘的
鐘的![]() 人進行統計,按照租車時間
人進行統計,按照租車時間![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分組做出頻率分布直方圖,并作出租用時間和莖葉圖(圖中僅列出了時間在
分組做出頻率分布直方圖,并作出租用時間和莖葉圖(圖中僅列出了時間在![]() ,
, ![]() 的數據).
的數據).

(1)求![]() 的頻率分布直方圖中的
的頻率分布直方圖中的![]() ;
;
(2)從租用時間在![]() 分鐘以上(含
分鐘以上(含![]() 分鐘)的人數中隨機抽取
分鐘)的人數中隨機抽取![]() 人,設隨機變量
人,設隨機變量![]() 表示所抽取的
表示所抽取的![]() 人租用時間在
人租用時間在![]() 內的人數,求隨機變量
內的人數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉行“青少年禁毒”知識競賽網上答題,高二年級共有500名學生參加了這次競賽.為了解本次競賽成績情況,從中抽取了100名學生的成績進行統計.請你解答下列問題: 
(1)根據下面的頻率分布表和頻率分布直方圖,求出a+d和b+c的值;
(2)若成績不低于90分的學生就能獲獎,問所有參賽學生中獲獎的學生約為多少人?
分組 | 頻數 | 頻率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合計 | 100 | d |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com