
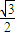 ,頂角的正弦值是底角正弦值的
,頂角的正弦值是底角正弦值的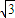 倍,則該三角形一腰的長為( )
倍,則該三角形一腰的長為( )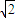
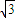
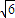
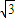 倍列出關系式,利用誘導公式及二倍角的正弦函數公式化簡,得到頂角一半的正弦值,利用特殊角的三角函數值求出頂角的度數,又設腰長為m,根據三角形的面積公式表示出三角形的面積S,讓面積等于
倍列出關系式,利用誘導公式及二倍角的正弦函數公式化簡,得到頂角一半的正弦值,利用特殊角的三角函數值求出頂角的度數,又設腰長為m,根據三角形的面積公式表示出三角形的面積S,讓面積等于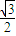 列出關于m的方程,求出方程的解即可得到m的值即為三角形的腰長.
列出關于m的方程,求出方程的解即可得到m的值即為三角形的腰長.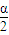 ,腰長為m,m>0,
,腰長為m,m>0,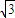 sin(90°-
sin(90°-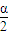 )=
)=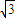 cos
cos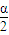 ,即2sin
,即2sin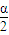 cos
cos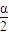 =
=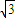 cos
cos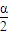 ,
,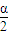 =
=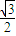 ,
,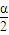 =60°,所以α=120°,
=60°,所以α=120°, m2sinα=
m2sinα=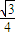 m2=
m2=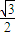 ,即m2=2,m>0,
,即m2=2,m>0,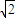 .
.

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2011年四川省綿陽市高考數學二模試卷(文科)(解析版) 題型:選擇題
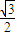 ,頂角的正弦值是底角正弦值的
,頂角的正弦值是底角正弦值的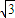 倍,則該三角形一腰的長為( )
倍,則該三角形一腰的長為( )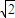

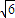
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com