
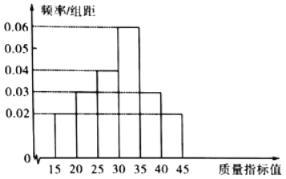
【題目】為了提高生產效益,某企業引進了一批新的生產設備,為了解設備生產產品的質量情況,分別從新、舊設備所生產的產品中,各隨機抽取100件產品進行質量檢測,所有產品質量指標值均在(15,45]以內,規定質量指標值大于30的產品為優質品,質量指標值在(15,30]的產品為合格品.舊設備所生產的產品質量指標值如頻率分布直方圖所示,新設備所生產的產品質量指標值如頻數分布表所示.
質量指標 | 頻數 |
(15,20] | 2 |
(20,25] | 8 |
(25,30] | 20 |
(30,35] | 30 |
(35,40] | 25 |
(40,45] | 15 |
合計 | 100 |
(1)請分別估計新、舊設備所生產的產品的優質品率.
(2)優質品率是衡量一臺設備性能高低的重要指標,優質品率越高說明設備的性能越高.根據已知圖表數據填寫下面列聯表(單位:件),并判斷是否有95%的把握認為“產品質量高與新設備有關”.
非優質品 | 優質品 | 合計 | |
新設備產品 | |||
舊設備產品 | |||
合計 |
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
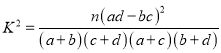 ,其中
,其中![]() .
.
(3)用頻率代替概率,從新設備所生產的產品中隨機抽取3件產品,其中優質品數為X件,求X的分布列及數學期望.
【答案】(1)70%,55%(2)見解析,有95%的把握認為“產品質量高與新設備有關”.(3)見解析,2.1
【解析】
(1)由頻數分布表可知,將(30,45]的頻數相加,再除以100,即為新設備的優質品率;由頻率分布直方圖可知,將(30,45]的頻率/組距相加,再乘以組距即為舊設備的優質品率;
(2)先填寫2×2列聯表,再根據![]() 的公式計算其觀測值,并與附表中的數據進行對比即可作出判斷;
的公式計算其觀測值,并與附表中的數據進行對比即可作出判斷;
(3)由(1)知,新設備所生產的優質品率為0.7,而X的所有可能取值為0,1,2,3,然后根據二項分布求概率的方式逐一求出每個X的取值所對應的概率即可得分布列,進而求得數學期望.
(1)估計新設備所生產的產品的優質品率為![]() ,
,
估計舊設備所生產的產品的優質品率為![]()
(2)補充完整的2×2列聯表如下所示,
非優質品 | 優質品 | 合計 | |
新設備產品 | 30 | 70 | 100 |
舊設備產品 | 45 | 55 | 100 |
合計 | 75 | 125 | 200 |
∴![]() ,
,
∴有95%的把握認為“產品質量高與新設備有關”.
(3)由(1)知,新設備所生產的優質品率為0.7,而X的所有可能取值為0,1,2,3,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∴X的分布列為:
X | 0 | 1 | 2 | 3 |
P | 0.027 | 0.189 | 0.441 | 0.343 |
數學期望![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數
,求實數![]() 的值;
的值;
(2)證明:當![]() 時,
時,![]() 在
在![]() 上有兩個極值點;
上有兩個極值點;
(3)設![]() ,若
,若![]() 在
在![]() 上是單調減函數(
上是單調減函數(![]() 為自然對數的底數),求實數
為自然對數的底數),求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某民航部門統計的2019年春運期間12個城市售出的往返機票的平均價格以及相比上年同期變化幅度的數據統計圖表如圖所示,根據圖表,下面敘述不正確的是( )
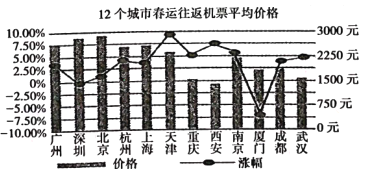
A. 同去年相比,深圳的變化幅度最小且廈門的平均價格有所上升
B. 天津的平均價格同去年相比漲幅最大且2019年北京的平均價格最高
C. 2019年平均價格從高到低居于前三位的城市為北京、深圳、廣州
D. 同去年相比,平均價格的漲幅從高到低居于前三位的城市為天津、西安、南京
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司年會有幸運抽獎環節,一個箱子里有相同的十個兵乓球,球上分別標0,1,2,…,9這十個自然數,每位員工有放回的依次取出三個球.規定:每次取出的球所標數字不小于后面取出的球所標數字即中獎.中獎獎項:三個數字全部相同中一等獎,獎勵10000元現金;三個數字中有兩個數字相同中二等獎,獎勵5000元現金;三個數字各不相同中三等獎,獎勵2000元現金;其它不中獎,沒有獎金.
(1)求員工A中二等獎的概率;
(2)設員工A中獎獎金為X,求X的分布列;
(3)員工B是優秀員工,有兩次抽獎機會,求員工B中獎獎金的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,![]() 軸的正半軸為極軸,以相同的長度單位建立極坐標系,已知直線
軸的正半軸為極軸,以相同的長度單位建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,![]()
(l)設![]() 為參數,若
為參數,若![]() ,求直線
,求直線![]() 的參數方程;
的參數方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 設
設![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】全民參與是打贏新型冠狀病毒防疫戰的根本方法.在防控疫情的過程中,某小區的“卡口”工作人員由“社區工作者”“下沉干部”“志愿者”三種身份的人員構成,其中社區工作者3人,下沉干部2人,志愿者1人.某電視臺某天上午隨機抽取2人進行訪談,某報社在該天下午隨機抽取1人進行訪談.
(1)設![]() 表示上午抽到的社區工作者的人數,求隨機變量
表示上午抽到的社區工作者的人數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(2)設![]() 為事件“全天抽到的
為事件“全天抽到的![]() 名工作人員的身份互不相同”,求事件
名工作人員的身份互不相同”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽籺,俗稱“粽子”,古稱“角黍”,是端午節大家都會品嘗的食品,傳說這是為了紀念戰國時期楚國大臣、愛國主義詩人屈原.如圖,平行四邊形形狀的紙片是由六個邊長為![]() 的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球表面積的最大值為____.
的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球表面積的最大值為____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com