解:(1)由題意可得“特征數(shù)”是{
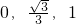
}的函數(shù)為y=
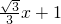
,
其圖象向下平移2個(gè)單位,得到的新函數(shù)的解析式是y=
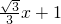
-2,即y=
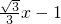
;
(2)由題意可知y=
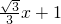
向下平移兩個(gè)單位得y=
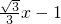
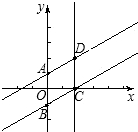
∴AD∥BC,且AB=2,由直線的方程可知AB∥CD.
∴四邊形ABCD為平行四邊形.
同時(shí)可得C點(diǎn)坐標(biāo)為(

,0),D(

,2)
由勾股定理可得BC=2,即AB=BC=2
∴四邊形ABCD為菱形.
(3)可得二次函數(shù)為:y=x
2-2bx+b
2+

,化為頂點(diǎn)式為:y=(x-b)
2+

,
∴二次函數(shù)的圖象不會(huì)經(jīng)過點(diǎn)B和點(diǎn)C.
設(shè)二次函數(shù)的圖象與四邊形有公共部分,
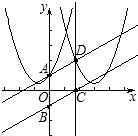
當(dāng)二次函數(shù)的圖象經(jīng)過點(diǎn)A時(shí),將A(0,1),代入二次函數(shù),
解得b=-

,b=

(不合題意,舍去),
當(dāng)二次函數(shù)的圖象經(jīng)過點(diǎn)D時(shí),將D(

,2),代入二次函數(shù),
解得b=

+

,b=
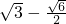
(不合題意,舍去),
所以實(shí)數(shù)b的取值范圍:
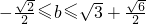
.
分析:(1)由題意可得函數(shù)解析式,由平移的知識(shí)可得;
(2)由直線的方程易證四邊形為平行四邊形,由坐標(biāo)可得AB=BC,即得菱形;
(3)分別求得函數(shù)圖象過點(diǎn)A,D時(shí)的b值,數(shù)形結(jié)合可得范圍.
點(diǎn)評(píng):本題考查新定義,涉及二次函數(shù)和直線的位置關(guān)系的判定,屬基礎(chǔ)題.

 定義{a,b,c}為函數(shù)y=ax2+bx+c的“特征數(shù)”.如:函數(shù)y=x2-2x+3的“特征數(shù)”是{1,-2,3},函數(shù)y=2x+3的“特征數(shù)”是{0,2,3,},函數(shù)y=-x的“特征數(shù)”是{0,-1,0}
定義{a,b,c}為函數(shù)y=ax2+bx+c的“特征數(shù)”.如:函數(shù)y=x2-2x+3的“特征數(shù)”是{1,-2,3},函數(shù)y=2x+3的“特征數(shù)”是{0,2,3,},函數(shù)y=-x的“特征數(shù)”是{0,-1,0}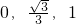 }的函數(shù)圖象向下平移2個(gè)單位,得到的新函數(shù)的解析式是________; (答案寫在答卷上)
}的函數(shù)圖象向下平移2個(gè)單位,得到的新函數(shù)的解析式是________; (答案寫在答卷上) 分別交于D、C兩點(diǎn),在平面直角坐標(biāo)系中畫出圖形,判斷以點(diǎn)A、B、C、D為頂點(diǎn)的四邊形形狀,并說明理由;
分別交于D、C兩點(diǎn),在平面直角坐標(biāo)系中畫出圖形,判斷以點(diǎn)A、B、C、D為頂點(diǎn)的四邊形形狀,并說明理由; }的函數(shù)圖象的有交點(diǎn),求滿足條件的實(shí)數(shù)b的取值范圍.
}的函數(shù)圖象的有交點(diǎn),求滿足條件的實(shí)數(shù)b的取值范圍.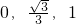 }的函數(shù)為y=
}的函數(shù)為y=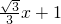 ,
,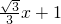 -2,即y=
-2,即y=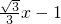 ;
;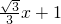 向下平移兩個(gè)單位得y=
向下平移兩個(gè)單位得y=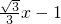

 ,0),D(
,0),D( ,2)
,2) ,化為頂點(diǎn)式為:y=(x-b)2+
,化為頂點(diǎn)式為:y=(x-b)2+ ,
,
 ,b=
,b= (不合題意,舍去),
(不合題意,舍去), ,2),代入二次函數(shù),
,2),代入二次函數(shù), +
+ ,b=
,b=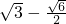 (不合題意,舍去),
(不合題意,舍去),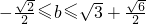 .
.


 定義{a,b,c}為函數(shù)y=ax2+bx+c的“特征數(shù)”.如:函數(shù)y=x2-2x+3的“特征數(shù)”是{1,-2,3},函數(shù)y=2x+3的“特征數(shù)”是{0,2,3,},函數(shù)y=-x的“特征數(shù)”是{0,-1,0}
定義{a,b,c}為函數(shù)y=ax2+bx+c的“特征數(shù)”.如:函數(shù)y=x2-2x+3的“特征數(shù)”是{1,-2,3},函數(shù)y=2x+3的“特征數(shù)”是{0,2,3,},函數(shù)y=-x的“特征數(shù)”是{0,-1,0}