函數y=loga(2-ax)在[0,1]上是減函數,則a的取值范圍是( )
A.(0,1)
B.(0,2)
C.(1,2)
D.(2,+∞)
【答案】
分析:a>0⇒2-ax在[0,1]上是減函數由復合函數的單調性可得a>1,在利用對數函數的真數須大于0可解得a的取值范圍.
解答:解:∵a>0,
∴2-ax在[0,1]上是減函數.
∴y=log
au應為增函數,且u=2-ax在[0,1]上應恒大于零.
∴
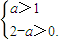
∴1<a<2.
故答案為:C.
點評:本題考查了對數函數與其它函數復合在一起的一新函數的單調性,復合函數的單調性遵循的原則是同增異減,即單調性相同復合在一起為增函數,單調性相反,復合在一起為減函數.
