
【題目】已知函數![]() ,
, ![]() .
.
(I)求![]() 的單調區間;
的單調區間;
(II)若對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)詳見解析;(2) ![]() .
.
【解析】試題分析:對函數求導,針對參數![]() 進行討論,研究函數得單調性;第二步為恒成立問題,當
進行討論,研究函數得單調性;第二步為恒成立問題,當![]() 時,由于
時,由于![]() 不滿足題意要求,當
不滿足題意要求,當![]() 時,求出函數
時,求出函數![]() 的最大值,要使
的最大值,要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,從而求出
,從而求出![]() 的范圍.
的范圍.
試題解析:(I)![]() , 當
, 當![]() 時,
時, ![]() 恒成立,則
恒成立,則![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,令
時,令![]() ,則
,則![]() .則
.則![]() 在區間
在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減.
上單調遞減.
(II)方法1:
當![]() 時,因為
時,因為![]() ,
,
所以不會有![]() ,
, ![]() .
.
②當![]() 時,由(I)知,
時,由(I)知, ![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
所以![]() ,
, ![]() 等價于
等價于![]() .即
.即![]() .
.
設![]() ,由(I)知
,由(I)知![]() 在
在![]() 上單調遞增.
上單調遞增.
又![]() ,所以
,所以![]() 的解為
的解為![]() .
.
故![]() ,
, ![]() 時,實數
時,實數![]() 的取值范圍是
的取值范圍是![]() .
.
方法2: ![]() ,
, ![]() 等價于
等價于![]() .令
.令![]() ,則
,則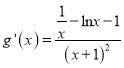 .
.
令![]() ,則
,則![]() .
.
因為當![]() ,
, ![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,可得
,可得![]() 和
和![]() 在
在![]() 上的情況如下:
上的情況如下:
|
|
|
|
| + | 0 | - |
| 單調遞增 | 單調遞減 |
所以![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
因此![]() ,
, ![]() 等價于
等價于![]() .
.
故![]() ,
, ![]() 時,實數
時,實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】下列三個集合:
①{x|y=x2+1};
②{y|y=x2+1};
③{(x,y)|y=x2+1}.
(1)它們是不是相同的集合?
(2)它們各自的含義是什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業常年生產一種出口產品,根據預測可知,進入21世紀以來,該產品的產量平穩增長.記2009年為第1年,且前4年中,第x年與年產量f(x) 萬件之間的關系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三種函數模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你認為最適合的函數模型,并說明理由,然后選取其中你認為最適合的數據求出相應的解析式;
(2)因遭受某國對該產品進行反傾銷的影響,2015年的年產量比預計減少30%,試根據所建立的函數模型,確定2015年的年產量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}
(1)若a=-2,求B∩A,B∩UA;
(2)若BA,求實數a取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() .(14分)
.(14分)
(1)此方程表示圓,求m的取值范圍;
(2)若(1)中的圓與直線x+2y-4=0相交于M、N兩點,且![]() (O為坐標原點),求m的值;
(O為坐標原點),求m的值;
(3)在(2)的條件下,求以![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為定義在R上的奇函數,當
為定義在R上的奇函數,當![]() 時,
時,![]() 為二次函數,且滿足
為二次函數,且滿足![]() ,
,![]() 在
在![]() 上的兩個零點為
上的兩個零點為![]() 和
和![]() .
.
(1)求函數![]() 在R上的解析式;
在R上的解析式;
(2)作出![]() 的圖象,并根據圖象討論關于
的圖象,并根據圖象討論關于![]() 的方程
的方程![]()
![]() 根的個數.
根的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】祖暅原理:“冪勢既同,則積不容異”.它是中國古代一個涉及幾何體體積的問題,意思是兩個同高的幾何體,如在等高處的截面積恒相等,則體積相等.設![]() 為兩個同高的幾何體,
為兩個同高的幾何體,![]() 的體積不相等,
的體積不相等,![]() 在等高處的截面積不恒相等,根據祖暅原理可知,
在等高處的截面積不恒相等,根據祖暅原理可知,![]() 是
是![]() 的( )
的( )
A. 充分不必要條件 B. 必要不充分條件
C. 充要條件 D. 既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com