Question

已知數列{a_n},{b_n}滿足：a₁=1,a₂=a(a為常數)，且b_n=a_n·a_n+1,其中n=1,2,3…

(1)若{a_n}是等比數列，試求數列{b_n}的前n項和S_n的公式；

(2)當{b_n}是等比數列時，甲同學說：{a_n}一定是等比數列；乙同學說：{a_n}一定不是等比數列，你認為他們的說法是否正確？為什么？

Answer 1

解:(1)∵{a_n}是等比數列a₁=1,a₂=a,?∴a≠0,a_n=a^n-1.

又b_n=a_n·a_n+1則b₁=a₁·a₂=a,===a²，

即{b_n}是以a為首項，a²為公比的等比數列._?

∴S_n=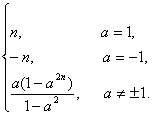

(2)甲、乙兩個同學的說法都不正確，理由如下._?

解法1：設{b_n}的公比為q,則===q且a≠0,

又a₁=1,a₂=a,a₁,a₃,a₅,…,a_2n-1,…是以1為首項，q為公比的等比數列，a₂,a₄,a₆,…,a_2n,…是以a為首項，q為公比的等比數列，即{a_n}為：1，a,q,aq,q²,aq²,_?

當q=a²時，{a_n}是等比數列；_?

當q≠a²時，{a_n}不是等比數列._?

解法2：{a_n}可能是等比數列，也可能不是等比數列，舉例說明如下：_?

設{b_n}的公比為q_?

①取a=q=1時，a_n=1(n∈N),此時b_n=a_na_n+1=1,{a_n}、{b_n}都是等比數列._?

②取a=2,q=1時，_?

a_n=b_n=2，n∈N.

所以{b_n}是等比數列，而{a_n}不是等比數列.