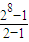已知在正項等比數列{an}中,a1=1,a2a4=16,則|a1-12|+|a2-12|+…+|a8-12|=( )
A.224
B.225
C.226
D.256
【答案】
分析:利用等比數列的通項公式即可得出公比q,得到通項公式.判斷a
n≤12成立時n的值,即可去掉絕對值符號,再利用等比數列的前n項和公式即可得出.
解答:解:設正項等比數列{a
n}的公比為q>0,∵a
1=1,a
2a
4=16,∴q
4=16,解得q=2.
∴
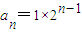
=2
n-1,
由2
n-1≤12,解得n≤4.
∴|a
1-12|+|a
2-12|+…+|a
8-12|=12-a
1+12-a
2+12-a
3+12-a
4+a
5-12+…+a
8-12
=-2(a
1+a
2+a
3+a
4)+(a
1+a
2+…+a
8)
=-
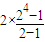
+
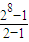
=-2(2
4-1)+2
8-1
=225.
故選B.
點評:判斷a
n≤12成立時n的值正確去掉絕對值符號,熟練掌握等比數列的通項公式、等比數列的前n項和公式是解題的關鍵.

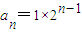 =2n-1,
=2n-1,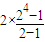 +
+