
【題目】2017年春晚分會場之一是涼山西昌,電視播出后,通過網絡對涼山分會場的表演進行了調查.調查分三類人群進行,參加了網絡調查的觀眾們的看法情況如下:
觀眾對涼山分會場表演的看法 | 非常好 | 好 |
中國人且非四川(人數比例) |
|
|
四川人(非涼山)(人數比例) |
|
|
涼山人(人數比例) |
|
|
(1)從這三類人群中各選一個人,求恰好有2人認為“非常好”的概率(用比例作為相應概率);
(2)若在四川人(非涼山)群中按所持態度分層抽樣,抽取9人,在這9人中任意選取3人,認為“非常好”的人數記為ξ,求ξ的分布列和數學期望.
【答案】
(1)解:設事件“恰好有2人認為“非常好””為A,則P(A)= ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
(2)解:若在四川人(非涼山)群中按所持態度分層抽樣,抽取9人,則其中認為“非常好”的人數為6,認為“好”的人數為3.在這9人中任意選取3人,認為“非常好”的人數記為ξ,則ξ的可能取值為:0,1,2,3.
P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() =
= ![]() .
.
∴ξ的分布列為:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(ξ)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =2.
=2.
【解析】(1)設事件“恰好有2人認為“非常好””為A,利用互相獨立與互斥事件的概率計算公式即可得出.(2)若在四川人(非涼山)群中按所持態度分層抽樣,抽取9人,則其中認為“非常好”的人數為6,認為“好”的人數為3.在這9人中任意選取3人,認為“非常好”的人數記為ξ,則ξ的可能取值為:0,1,2,3.利用“超幾何分布列”的概率計算公式及其數學期望計算公式即可得出.
【考點精析】通過靈活運用離散型隨機變量及其分布列,掌握在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列即可以解答此題.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 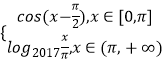 ,若有三個不同的實數a,b,c,使得f(a)=f(b)=f(c),則a+b+c的取值范圍為( )
,若有三個不同的實數a,b,c,使得f(a)=f(b)=f(c),則a+b+c的取值范圍為( )
A.(2π,2017π)
B.(2π,2018π)
C.( ![]() ,
, ![]() )
)
D.(π,2017π)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義[x]表示不超過x的最大整數,例如[2.11]=2,[﹣1.39]=﹣2,執行如下圖所示的程序框圖,則輸出m的值為 ( )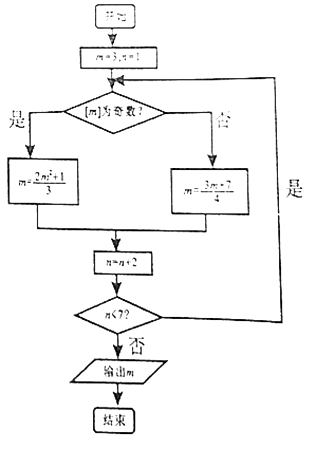
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,數列{bn}是等比數列,Sn是數列{an}的前n項和,a1=b1=1,S2=![]() .
.
(1)若b2是a1,a3的等差中項,求數列{an}與{bn}的通項公式;
(2)若an∈N+,數列{![]() }是公比為9的等比數列,求證:
}是公比為9的等比數列,求證:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點M到點
中,點M到點![]() 的距離比它到
的距離比它到![]() 軸的距離大2,記點M的軌跡為C.
軸的距離大2,記點M的軌跡為C.
(1)求軌跡C的方程;
(2)若直線![]() 與軌跡C恰有2個公共點,求實數b的取值范圍.
與軌跡C恰有2個公共點,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,其中m,n,k∈R.
,其中m,n,k∈R.
(1)若m=n=k=1,求f(x)的單調區間;
(2)若n=k=1,且當x≥0時,f(x)≥1總成立,求實數m的取值范圍;
(3)若m>0,n=0,k=1,若f(x)存在兩個極值點x1、x2 , 求證: ![]() <f(x1)+f(x2)<
<f(x1)+f(x2)< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線y2=2px(p>0)的焦點為F,A(x1,y1),B(x2,y2)是過F的直線與拋物線的兩個交點,求證:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 為定值;
為定值;
(3)以AB為直徑的圓與拋物線的準線相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=aex﹣x(a∈R),其中e為自然對數的底數,e=2.71828…
(Ⅰ)判斷函數f(x)的單調性,并說明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com