
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,直線
軸的正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 至多只有一個公共點,求實數
至多只有一個公共點,求實數![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() ,
,![]() 的中點為
的中點為![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)利用參數方程、極坐標方程與直角坐標方程的互化公式把曲線![]() 和直線
和直線![]() 的方程化為直角坐標方程,并聯立直線
的方程化為直角坐標方程,并聯立直線![]() 和曲線
和曲線![]() 的直角坐標方程,得到關于
的直角坐標方程,得到關于![]() 的一元二次方程,利用判別式
的一元二次方程,利用判別式![]() 即可求出實數
即可求出實數![]() 的取值范圍;
的取值范圍;
![]() 根據題意,設
根據題意,設![]() ,
,![]() ,
,![]() 的中點
的中點![]() 為
為![]() ,直線
,直線![]() 和曲線
和曲線![]() 的直角坐標方程聯立,得到關于
的直角坐標方程聯立,得到關于![]() 的一元二次方程,由兩個交點
的一元二次方程,由兩個交點![]() ,
,![]() 可得判別式
可得判別式![]() ,求出
,求出![]() 取值范圍,利用韋達定理和點
取值范圍,利用韋達定理和點![]() 在直線
在直線![]() 上表示出點
上表示出點![]() 坐標,消去參數
坐標,消去參數![]() 即可求出
即可求出![]() ,
,![]() 的中點
的中點![]() 的軌跡方程.
的軌跡方程.
(1)因為曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),
消去參數![]() 可得,曲線
可得,曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
由題意知,直線![]() 的極坐標方程可化為
的極坐標方程可化為![]() ,
,
因為![]() ,所以直線
,所以直線![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
聯立方程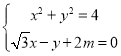 ,可得
,可得![]() ,
,
因為直線![]() 與曲線
與曲線![]() 至多只有一個公共點,
至多只有一個公共點,
所以判別式![]() ,解得
,解得![]() 或
或![]() ,
,
所以所求實數![]() 的取值范圍為
的取值范圍為![]() 或
或![]() .
.
(2)設![]() ,
,![]() ,
,![]() 的中點
的中點![]() 為
為![]() ,
,
聯立方程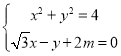 ,可得
,可得![]() ,
,
所以判別式![]() ,解得
,解得![]() ,
,
由韋達定理可得,![]() ,
,
因為點![]() 在直線
在直線![]() 上,所以
上,所以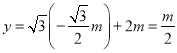 ,
,
所以可得![]() ,
,![]() 即為點
即為點![]() 的軌跡方程.
的軌跡方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
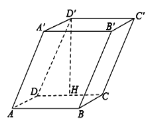
【題目】如圖,在棱柱![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形,![]()
![]() ,
,![]() ,且
,且![]() 在底面上的投影
在底面上的投影![]() 恰為
恰為![]() 的中點.
的中點.
(1)過![]() 作與
作與![]() 垂直的平面
垂直的平面![]() ,交棱
,交棱![]() 于點
于點![]() ,試確定點
,試確定點![]() 的位置,并說明理由;
的位置,并說明理由;
(2)若點![]() 滿足
滿足![]() ,試求
,試求![]() 的值,使二面角
的值,使二面角![]() 為
為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次數學測驗共有12道選擇題,每道題共有四個選項,且其中只有一個選項是正確的,評分標準規定:每選對1道題得5分,不選或選錯得0分. 在這次數學測驗中,考生甲每道選擇題都按照規則作答,并能確定其中有9道題能選對;其余3道題無法確定正確選項,在這3道題中,恰有2道能排除兩個錯誤選項,另1題只能排除一個錯誤選項. 若考生甲做這3道題時,每道題都從不能排除的選項中隨機挑選一個選項作答,且各題作答互不影響.在本次測驗中,考生甲選擇題所得的分數記為![]()
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 經過點
經過點![]() 且傾斜角為
且傾斜角為![]() .
.
(1)求曲線![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的參數方程;
的參數方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,滿足
,滿足![]() 為
為![]() 的中點,求
的中點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年末,武漢出現新型冠狀病毒肺炎(![]() )疫情,并快速席卷我國其他地區,傳播速度很快.因這種病毒是以前從未在人體中發現的冠狀病毒新毒株,所以目前沒有特異治療方法,防控難度很大.武漢市出現疫情最早,感染人員最多,防控壓力最大,武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者、疑似的新冠肺炎患者、無法明確排除新冠肺炎的發熱患者和與確診患者的密切接觸者等“四類”人員,強化網格化管理,不落一戶、不漏一人.在排查期間,一戶6口之家被確認為“與確診患者的密切接觸者”,這種情況下醫護人員要對其家庭成員隨機地逐一進行“核糖核酸”檢測,若出現陽性,則該家庭為“感染高危戶”.設該家庭每個成員檢測呈陽性的概率均為
)疫情,并快速席卷我國其他地區,傳播速度很快.因這種病毒是以前從未在人體中發現的冠狀病毒新毒株,所以目前沒有特異治療方法,防控難度很大.武漢市出現疫情最早,感染人員最多,防控壓力最大,武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者、疑似的新冠肺炎患者、無法明確排除新冠肺炎的發熱患者和與確診患者的密切接觸者等“四類”人員,強化網格化管理,不落一戶、不漏一人.在排查期間,一戶6口之家被確認為“與確診患者的密切接觸者”,這種情況下醫護人員要對其家庭成員隨機地逐一進行“核糖核酸”檢測,若出現陽性,則該家庭為“感染高危戶”.設該家庭每個成員檢測呈陽性的概率均為![]() (
(![]() )且相互獨立,該家庭至少檢測了5個人才能確定為“感染高危戶”的概率為
)且相互獨立,該家庭至少檢測了5個人才能確定為“感染高危戶”的概率為![]() ,當
,當![]() 時,
時,![]() 最大,則
最大,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩種樹苗中各抽測了10株樹苗的高度,其莖葉圖如圖.根據莖葉圖,下列描述正確的是( )
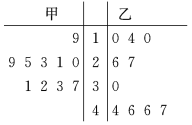
A.甲種樹苗的平均高度大于乙種樹苗的平均高度,且甲種樹苗比乙種樹苗長得整齊
B.甲種樹苗的平均高度大于乙種樹苗的平均高度,但乙種樹苗比甲種樹苗長得整齊
C.乙種樹苗的平均高度大于甲種樹苗的平均高度,且乙種樹苗比甲種樹苗長得整齊
D.乙種樹苗的平均高度大于甲種樹苗的平均高度,但甲種樹苗比乙種樹苗長得整齊
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com