【題目】已知三棱錐
的底面
為正三角形，頂點在底面上的射影為底面的中心，
，
分別是棱
，
的中點，且
，若側棱
，則三棱錐的外接球的表面積是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
由題意推出MN⊥平面SAC，即SB⊥平面SAC，∠ASB＝∠BSC＝∠ASC＝90°，將此三棱錐補成正方體，則它們有相同的外接球，正方體的對角線就是球的直徑，求出直徑即可求出球的表面積．
解：∵M，N分別為棱SC，BC的中點，∴MN∥SB
∵三棱錐S﹣ABC為正棱錐，
∴SB⊥AC（對棱互相垂直），∴MN⊥AC
又∵MN⊥AM，而AM∩AC＝A，
∴MN⊥平面SAC，∴SB⊥平面SAC
∴∠ASB＝∠BSC＝∠ASC＝90°
以SA，SB，SC為從同一定點S出發的正方體三條棱，
將此三棱錐補成以正方體，則它們有相同的外接球，
正方體的對角線就是球的直徑．∴2R
SA＝6，∴R＝3，
∴S＝4πR2＝36π．
故選：C．
科目：高中數學 來源： 題型：
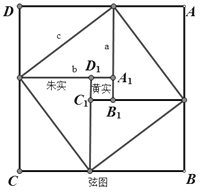
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”，三國時期吳國的數學家趙爽在《周髀算經》中注釋了其理論證明，其基本思想是圖形經過割補后面積不變.即通過如圖所示的“弦圖”，將勻股定理表述為：“勾股各自乘，并之，為弦實，開方除之，即弦”（其中
分別為勾股弦）；證明方法敘述為：“按弦圖，又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實”，即
，化簡得
.現已知
，
，向外圍大正方形
區域內隨機地投擲一枚飛鏢，飛鏢落在中間小正方形
內的概率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
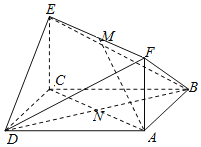
【題目】如圖，已知正方形
和矩形
所在的平面互相垂直，
，
，
是線段
的中點．
（1）求證
平面
；
（2）求二面角
的大小；
（3）試在線段
上一點
，使得
與
所成的角是60°．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出以下結論：
①命題“若
，則
”的逆否命題“若
，則
”；
②“”是“
”的充分條件；
③命題“若
，則方程
有實根”的逆命題為真命題；
④命題“若
，則
且
”的否命題是真命題.
其中錯誤的是__________.（填序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高血壓高血糖和高血脂統稱“三高”.如圖是西南某地區從2010年至2016年患“三高”人數y(單位：千人)的折線圖.
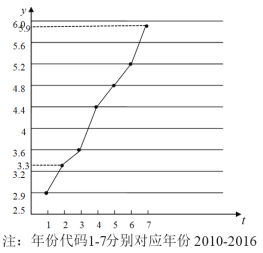
（1）由折線圖看出，可用線性回歸模型擬合
與
的關系，請求出相關系數(精確到0.01)并加以說明；
（2）建立關于的回歸方程，預測2018年該地區患“三高”的人數.
參考數據：
，
，
，
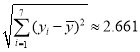.參考公式：相關系數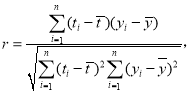
回歸方程
中斜率和截距的最小二乘法估計公式分別為：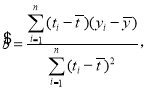
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】微信是騰訊公司推出的一種手機通訊軟件，一經推出便風靡全國，甚至涌現出一批在微信的朋友圈內銷售商品的人（被稱為微商）.為了調查每天微信用戶使用微信的時間，某經銷化妝品的微商在一廣場隨機采訪男性、女性用戶各50名，其中每天玩微信超過6小時的用戶為“
組”，否則為“
組”，調查結果如下：
（1）根據以上數據，能否有60%的把握認為“組”用戶與“性別”有關？
（2）現從調查的女性用戶中按分層抽樣的方法選出5人贈送營養面膜1份，求所抽取5人中“組”和“組”的人數；
（3）從（2）中抽取的5人中再隨機抽取3人贈送200元的護膚品套裝，記這3人中在“組”的人數為
，試求的分布列與數學期望.
參考公式：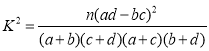 
，其中
.
臨界值表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某花卉經銷商銷售某種鮮花，售價為每支5元，成本為每支2元．銷售宗旨是當天進貨當天銷售．當天未售出的當垃圾處理．根據以往的銷售情況，按
進行分組，得到如圖所示的頻率分布直方圖．
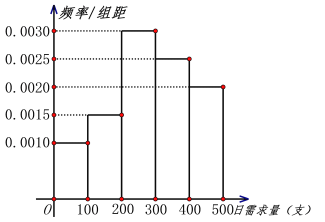
（1）根據頻率分布直方圖計算該種鮮花日需求量的平均數
,同一組中的數據用該組區間中點值代表；
（2）該經銷商某天購進了400支這種鮮花，假設當天的需求量為x枝，
，利潤為y元，求
關于
的函數關系式，并結合頻率分布直方圖估計利潤不小于800元的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
