
已知函數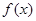 =
=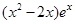 (e為自然對數的底數)
(e為自然對數的底數)
(Ⅰ)求函數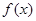 單調遞增區間;(5分)
單調遞增區間;(5分)
(Ⅱ)若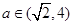 ,求函數
,求函數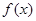 在區間[0,
在區間[0,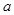 ]上的最大值和最小值.(5分)
]上的最大值和最小值.(5分)
(III) 若函數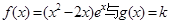 的圖象有三個不同的交點,求實數k的取值范圍.
的圖象有三個不同的交點,求實數k的取值范圍.
(參考數據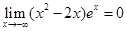 )(2分)
)(2分)
解:(Ⅰ)對函數 求導,得
求導,得 =ex(x2-2).-----2分
=ex(x2-2).-----2分
∵ex>0. ∴g(x)=x2-2在(-∞,- )和(
)和( ,+∞)上的函數值大于零,g(x)=x2-2在(
,+∞)上的函數值大于零,g(x)=x2-2在( -,
-, )上函數值小于零.
)上函數值小于零.
函數 單調遞增區間為(-∞,-
單調遞增區間為(-∞,- ),(
),( ,+∞) --5分
,+∞) --5分
(Ⅱ)①當 <
< ≤2時,
≤2時,
∵由(Ⅰ)得 在 [0,
在 [0, ]上遞減,
]上遞減, 在(
在( ,
, )上遞增,且
)上遞增,且 =
= =0,
=0,
∴ 在[0,
在[0, ]上的最大值為
]上的最大值為 =0,
=0,
 在區間[0,
在區間[0, ]上的最小值為
]上的最小值為 =(2-2
=(2-2 )e
)e .
.
------------8分
② 當 時,
時,
∵由(Ⅰ)得 在[0,
在[0, ]上遞減,
]上遞減, 在(
在( ,
, )上遞增,且
)上遞增,且 >
> ,
,
∴ 在[0,
在[0, ]上的最大值為
]上的最大值為 =(a2-2a)ea,
=(a2-2a)ea,
 在區間[0,
在區間[0, ]上的最小值為
]上的最小值為 =(2-2
=(2-2 )e
)e .
.
------------10分
(III) 實數k的取值范圍是(0,(2+2 )e
)e )
)
------------12分
【解析】略


科目:高中數學 來源:山東省濟寧市2012屆高三第一次高考模擬數學理科試題 題型:044
已知函數![]() ,其中e為自然對數的底數
,其中e為自然對數的底數
(Ⅰ)若函數g(x)在點(1,g(1))處的切線與直線2x-y+1=0垂直,求實數a的值;
(Ⅱ)若f(x)在[-1,1]上是單調增函數,求實數a的取值范圍;
(Ⅲ)當a=0時,求整數k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知x>![]() ,函數f(x)=x2,h(x)=2elnx(e為自然常數).
,函數f(x)=x2,h(x)=2elnx(e為自然常數).
(1)求證:f(x)≥h(x);
(2)若f(x)≥h(x)且g(x)≤h(x)恒成立,則稱函數h(x)的圖像為函數f(x),g(x)的“邊界”.已知函數g(x)=-4x2+px+q(p,q∈R),試判斷“函數f(x),g(x)以函數h(x)的圖像為邊界”和“函數f(x),g(x)的圖像有且僅有一個公共點”這兩個條件能否同時成立?若能同時成立,請求出實數p、q的值;若不能同時成立,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)已知函數f(x)=![]() (e為自然對數的底數),g(x)=
(e為自然對數的底數),g(x)=
f(x)-b,其中曲線f(x)在(0,f(0))處的切線斜率為-3.
(Ⅰ)求函數f(x)的單調區間;
(Ⅱ)設方程g(x)=0有且僅有一個實根,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)已知函數f(x)=![]() (e為自然對數的底數),g(x)=
(e為自然對數的底數),g(x)=
f(x)-b,其中曲線f(x)在(0,f(0))處的切線斜率為-3.
(Ⅰ)求函數f(x)的單調區間;
(Ⅱ)設方程g(x)=0有且僅有一個實根,求實數b的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com