
���}Ŀ����(du��)������![]() ������(sh��)��
������(sh��)��![]() �M��
�M��![]() ���t�Q�@��(g��)��(sh��)�О顰K��(sh��)�С�.
���t�Q�@��(g��)��(sh��)�О顰K��(sh��)�С�.
��1����֪��(sh��)�У�1��![]() ��
��![]() �ǡ�K��(sh��)�С�����(sh��)��(sh��)m��ȡֵ������
�ǡ�K��(sh��)�С�����(sh��)��(sh��)m��ȡֵ������
��2���Ƿ�������(xi��ng)��-1�ğo(w��)�F�Ȳ(sh��)��![]() �顰K��(sh��)�С�������ǰn�(xi��ng)��
�顰K��(sh��)�С�������ǰn�(xi��ng)��![]() �M�㣺
�M�㣺![]() �������ڣ����
�������ڣ����![]() ��ͨ�(xi��ng)��ʽ���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��ͨ�(xi��ng)��ʽ���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��3����֪���(xi��ng)����������(sh��)�ĵȱȔ�(sh��)��![]() ��������4�(xi��ng)���顰K��(sh��)�С�����(sh��)��
��������4�(xi��ng)���顰K��(sh��)�С�����(sh��)��![]() ���ǡ�K��(sh��)�С�����
���ǡ�K��(sh��)�С�����![]() ���Ƿ����
���Ƿ����![]() ��ʹ
��ʹ![]() �顰K��(sh��)�С��������ڣ�Ո(q��ng)�����
�顰K��(sh��)�С��������ڣ�Ո(q��ng)�����![]() �������ڣ�Ո(q��ng)�f(shu��)������.
�������ڣ�Ո(q��ng)�f(shu��)������.
���𰸡���1��![]() ��2���@�ӵĵȲ(sh��)��
��2���@�ӵĵȲ(sh��)��![]() �����ڣ�ԔҊ(ji��n)������3���𰸲�Ψһ�����wҊ(ji��n)����
�����ڣ�ԔҊ(ji��n)������3���𰸲�Ψһ�����wҊ(ji��n)����
��������
(1)ֱ�Ӹ���(j��)��K��(sh��)�С��Ķ��x�г��P(gu��n)��![]() �IJ���ʽ��⼴��.
�IJ���ʽ��⼴��.
(2) ���O(sh��)���ڵȲ(sh��)��![]() ����Ҫ��,�O(sh��)�����d,�����
����Ҫ��,�O(sh��)�����d,�����![]() ,������
,������![]() ��������
��������![]() �M��ėl���Ƿ��܉��������.
�M��ėl���Ƿ��܉��������.
(3) �O(sh��)��(sh��)��![]() �Ĺ��Ȟ�q,
�Ĺ��Ȟ�q,![]() ,�ٸ���(j��)�ȱȔ�(sh��)��
,�ٸ���(j��)�ȱȔ�(sh��)��![]() �顰K��(sh��)�С�,��(sh��)��
�顰K��(sh��)�С�,��(sh��)��![]() ���ǡ�K��(sh��)�С����ǰ���(xi��ng)���P(gu��n)ϵ,�ٸ���(j��)ǰ���(xi��ng)���P(gu��n)ϵ����rӑՓ�Ƿ��܉�M��
���ǡ�K��(sh��)�С����ǰ���(xi��ng)���P(gu��n)ϵ,�ٸ���(j��)ǰ���(xi��ng)���P(gu��n)ϵ����rӑՓ�Ƿ��܉�M��![]() �顰K��(sh��)�С�����.
�顰K��(sh��)�С�����.
(1)���}���![]() ,��
,��![]() ,��
,��
��ٵ�![]() ����ڵ�
����ڵ�![]() ��
��![]() .
.
����![]() ,�ʌ�(sh��)��(sh��)m��ȡֵ������
,�ʌ�(sh��)��(sh��)m��ȡֵ������![]() .
.
(2)���O(sh��)���ڵȲ(sh��)��![]() ����Ҫ��,�O(sh��)�����d,�t
����Ҫ��,�O(sh��)�����d,�t![]() ,
,
��![]() ,��
,��![]() ,
,
���}��,��![]() ��(du��)
��(du��)![]() ������,
������,
��![]() .
.
�ٮ�(d��ng)![]() �r(sh��),
�r(sh��),![]() ��
��
�ڮ�(d��ng)![]() �r(sh��),
�r(sh��),![]() ,
,
��?y��n)?/span>![]() ,
,
����![]() ,�c
,�c![]() �,
�,
���@�ӵĵȲ(sh��)��![]() ������.
������.
(3)�O(sh��)��(sh��)��![]() �Ĺ��Ȟ�q,�t
�Ĺ��Ȟ�q,�t![]() ,
,
��?y��n)?/span>![]() ��ÿһ�(xi��ng)����������(sh��),��
��ÿһ�(xi��ng)����������(sh��),��![]() ,
,
����![]() ,��
,��![]() .
.
��?y��n)?/span>![]() ,
,
������![]() ��,��
��,��![]() �������(xi��ng),
�������(xi��ng),
ͬ��,��![]() ��,
��,![]() �����(xi��ng).
�����(xi��ng).
��![]() �顰K��(sh��)�С�,ֻ��
�顰K��(sh��)�С�,ֻ��![]() ,��
,��![]() ,
,
����?y��n)?/span>![]() ���ǡ�K��(sh��)�С�,�ҡ�
���ǡ�K��(sh��)�С�,�ҡ�![]() ������С�(xi��ng),����
�������(xi��ng),����![]() ,��
,��![]() ,
,
�ɔ�(sh��)��![]() ��ÿһ�(xi��ng)����������(sh��),�ɵ�
��ÿһ�(xi��ng)����������(sh��),�ɵ�![]() ,
,
����![]() ,
,![]() ��
��![]() ,
,![]() ,
,
�ٮ�(d��ng)![]() ,
,![]() �r(sh��),
�r(sh��),![]() ,�t
,�t![]() ,
,
��![]() ,�t
,�t![]() ,
,
��![]() ,
,
����![]() ���f����(sh��)��,��
���f����(sh��)��,��![]() ,
,
����![]() ,
,
��?y��n)?/span>![]() ,
,
���Ԍ�(du��)�����![]() ,����
,����![]() ,
,
����(sh��)��![]() �顰K��(sh��)�С�.
�顰K��(sh��)�С�.
�ڮ�(d��ng)![]() ,
,![]() �r(sh��),
�r(sh��),![]() ,�t
,�t![]() .��?y��n)?/span>
.��?y��n)?/span>![]() ,
,
���Ԕ�(sh��)��![]() ���ǡ�K��(sh��)�С�.
���ǡ�K��(sh��)�С�.
�C�ϣ���(d��ng)![]() �r(sh��),��(sh��)��
�r(sh��),��(sh��)��![]() �顰K��(sh��)�С�,
�顰K��(sh��)�С�,
��(d��ng)![]() �r(sh��),��(sh��)��
�r(sh��),��(sh��)��![]() ���ǡ�K��(sh��)�С�.
���ǡ�K��(sh��)�С�.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() �c(di��n)��
�c(di��n)��![]() ��E�A�ϵ�һ��(d��ng)�c(di��n)��
��E�A�ϵ�һ��(d��ng)�c(di��n)��![]() ��e�����ֵ��
��e�����ֵ��![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() ���E�A�صõľ��Ξ�
���E�A�صõľ��Ξ�![]() ����(d��ng)
����(d��ng)![]() �S�r(sh��)��
�S�r(sh��)��![]() ��
��
(1)��E�A![]() �ķ��̣�
�ķ��̣�
(2)�E�A![]() ����ȡ���c(di��n)A��B����
����ȡ���c(di��n)A��B����![]() ��
��![]() ����߅��ƽ����߅��
����߅��ƽ����߅��![]() ����
����![]() ���t
���t![]() �Ƿ�鶨ֵ�����ǣ������ֵ���粻�ǣ�Ո(q��ng)�f(shu��)�����ɣ�
�Ƿ�鶨ֵ�����ǣ������ֵ���粻�ǣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���P(gu��n)�ں���(sh��)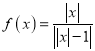 ���o�������Ă�(g��)���}�����������}����̖(h��o)��_______.
���o�������Ă�(g��)���}�����������}����̖(h��o)��_______.
��![]() �r(sh��)��
�r(sh��)��![]() ���{(di��o)�f�p�қ](m��i)����ֵ��
���{(di��o)�f�p�қ](m��i)����ֵ��
�ڷ���![]() һ���н⣻
һ���н⣻
���������![]() �н⣬�t��Ă�(g��)��(sh��)һ����ż��(sh��)��
�н⣬�t��Ă�(g��)��(sh��)һ����ż��(sh��)��
��![]() ��ż����(sh��)������Сֵ.
��ż����(sh��)������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
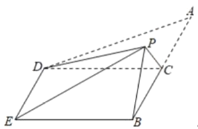
���}Ŀ����D����ֱ������![]() �У�
��![]() ,�c(di��n)
,�c(di��n)![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ,�F(xi��n)��������
,�F(xi��n)��������![]() ��
��![]() ����ʹ�c(di��n)
����ʹ�c(di��n)![]() ���_(d��)�c(di��n)
���_(d��)�c(di��n)![]() ��λ�ã���
��λ�ã���![]() �cƽ��
�cƽ��![]() ���ɵĽǞ�
���ɵĽǞ�![]() .
.
(1)���C:ƽ��![]() ƽ��
ƽ��![]() ;
;
(2)������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������}�M��14�֣����}����2��(g��)С�}����1С�}�M��6�֣���2С�}�M��8��.
�Еr(sh��)���ú���(sh��)
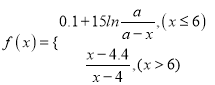
�����W(xu��)��(x��)ij�W(xu��)��֪�R(sh��)�����ճ̶ȣ�����x��ʾij�W(xu��)��֪�R(sh��)�ČW(xu��)��(x��)�Δ�(sh��)��![]() ����
����![]() ��ʾ��(du��)ԓ�W(xu��)��֪�R(sh��)�����ճ̶ȣ�����(sh��)��(sh��)a�c�W(xu��)��֪�R(sh��)���P(gu��n).
��ʾ��(du��)ԓ�W(xu��)��֪�R(sh��)�����ճ̶ȣ�����(sh��)��(sh��)a�c�W(xu��)��֪�R(sh��)���P(gu��n).
��1�� �C������(d��ng)![]() �r(sh��)�����ճ̶ȵ�������
�r(sh��)�����ճ̶ȵ�������![]() �����½���
�����½���
��2�� ����(j��)��(j��ng)�(y��n)���W(xu��)�Ƽס��ҡ�����(du��)��(y��ng)��a��ȡֵ�^(q��)�g�քe��![]() ,
,![]() ,
,
![]() .��(d��ng)�W(xu��)��(x��)ij�W(xu��)��֪�R(sh��)6�Εr(sh��)�����ճ̶���85%��Ո(q��ng)�_������(y��ng)�ČW(xu��)��.
.��(d��ng)�W(xu��)��(x��)ij�W(xu��)��֪�R(sh��)6�Εr(sh��)�����ճ̶���85%��Ո(q��ng)�_������(y��ng)�ČW(xu��)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��).
����Ȼ��(du��)��(sh��)�ĵה�(sh��).
��1����(d��ng)![]() �r(sh��)���C����
�r(sh��)���C����![]() ��
��![]() ��
��
��2��������(sh��)![]() ��
��![]() �ϴ��ڃɂ�(g��)�Oֵ�c(di��n)����(sh��)��(sh��)
�ϴ��ڃɂ�(g��)�Oֵ�c(di��n)����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij��˾��ӭ�������(hu��)���e�г骄(ji��ng)���(d��ng)���мס��҃ɂ�(g��)�骄(ji��ng)�������T���x��
�����ף�?ji��n)T������Ѓɴγ骄(ji��ng)�C(j��)��(hu��)��ÿ�γ骄(ji��ng)���Ъ�(ji��ng)�ʞ�![]() .��һ�γ骄(ji��ng)����δ�Ъ�(ji��ng)���t�骄(ji��ng)�Y(ji��)��.���Ъ�(ji��ng)���tͨ�^(gu��)��һö�|(zh��)�ؾ����Ӳ�ţ��Q���Ƿ��^�m(x��)�M(j��n)�еڶ��γ骄(ji��ng)��Ҏ(gu��)����������Ӳ�ţ����泯�ϣ��T���t�@��500Ԫ��(ji��ng)�𣬲��M(j��n)�еڶ��γ骄(ji��ng)�������泯�ϣ��T���t��M(j��n)�еڶ��γ骄(ji��ng)�����ڵڶ��γ骄(ji��ng)�У����Ъ�(ji��ng)���@�ê�(ji��ng)��1000Ԫ����δ�Ъ�(ji��ng)���t���@��(ji��ng)���0Ԫ.
.��һ�γ骄(ji��ng)����δ�Ъ�(ji��ng)���t�骄(ji��ng)�Y(ji��)��.���Ъ�(ji��ng)���tͨ�^(gu��)��һö�|(zh��)�ؾ����Ӳ�ţ��Q���Ƿ��^�m(x��)�M(j��n)�еڶ��γ骄(ji��ng)��Ҏ(gu��)����������Ӳ�ţ����泯�ϣ��T���t�@��500Ԫ��(ji��ng)�𣬲��M(j��n)�еڶ��γ骄(ji��ng)�������泯�ϣ��T���t��M(j��n)�еڶ��γ骄(ji��ng)�����ڵڶ��γ骄(ji��ng)�У����Ъ�(ji��ng)���@�ê�(ji��ng)��1000Ԫ����δ�Ъ�(ji��ng)���t���@��(ji��ng)���0Ԫ.
�����ң�?ji��n)T���B�m(x��)���γ骄(ji��ng)��ÿ���Ъ�(ji��ng)�ʾ���![]() ��ÿ���Ъ�(ji��ng)���ɫ@��(ji��ng)��400Ԫ.
��ÿ���Ъ�(ji��ng)���ɫ@��(ji��ng)��400Ԫ.
��1����ij�T���x�����M(j��n)�г骄(ji��ng)���@��(ji��ng)��![]() ��Ԫ���ķֲ��У�
��Ԫ���ķֲ��У�
��2��ij�T���x�����c�x�����M(j��n)�г骄(ji��ng)��ԇ���^�Ă�(g��)���������㣿
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ��
��![]() ��E�A
��E�A![]() ��
��![]() �����ҽ��c(di��n)���x���ʞ�
�����ҽ��c(di��n)���x���ʞ�![]() ���ҙE�A
���ҙE�A![]() ������c(di��n)��������c(di��n)�ľ��x֮�͞�
������c(di��n)��������c(di��n)�ľ��x֮�͞�![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() ���E�A��
���E�A��![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() ��ֱ���ĈA�^(gu��)
��ֱ���ĈA�^(gu��)![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)�ֱ��![]() ��ֱ��
��ֱ��![]() �S���c�E�A
�S���c�E�A![]() ����
����![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() .
.
��1�����c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ���c����
���c����![]() �������c(di��n)
�������c(di��n)![]() ��
��![]() ������(bi��o)ԭ�c(di��n)����
������(bi��o)ԭ�c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com