【題目】為了解電視對生活的影響，一個社會調查機構就平均每天看電視的時間調查了某地10000位居民，并根據所得數據畫出樣本的頻率分布直方圖（如圖），為了分析該地居民平均每天看電視的時間與年齡、學歷、職業等方面的關系，要從這10000位居民中再用分層抽樣抽出100位居民做進一步調查，則在
（小時）時間段內應抽出的人數是（ ）
A.25B.30C.50D.75
科目：高中數學 來源： 題型：
【題目】某小組為了研究晝夜溫差對一種稻谷種子發芽情況的影響，他們分別記錄了4月1日至4月5日的每天星夜溫差與實驗室每天每100顆種子的發芽數，得到如下資料：
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
溫差 | 9 | 10 | 11 | 8 | 12 |
發芽數 | 38 | 30 | 24 | 41 | 17 |
利用散點圖，可知
線性相關。
（1）求出
關于
的線性回歸方程，若4月6日星夜溫差
，請根據你求得的線性同歸方程預測4月6日這一天實驗室每100顆種子中發芽顆數；
（2）若從4月1日
4月5日的五組實驗數據中選取2組數據，求這兩組恰好是不相鄰兩天數據的概率.
（公式：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A＝{x|2≤x≤8}，B＝{x|1<x<6}，C＝{x|x>a}，U＝R．
(1)求A∪B，(CUA)∩B；
(2)若A∩C≠
，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數：f（x）＝x2﹣mx﹣n（m, n∈R）．
（1）若m+n＝0，解關于x的不等式f（x）≥x（結果用含m式子表示）；
（2）若存在實數m，使得當x∈[1，2]時，不等式x≤f（x）≤4x恒成立，求實數n的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設點
的坐標分別為
，直線
相交于點
，且它們的斜率之積是
.
（1）求點
的軌跡
的方程；
（2）直線
與曲線
相交于
兩點，若
是否存在實數
，使得
的面積為
?若存在，請求出
的值；若不存在，請說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為增強市民節能環保意識，某市面向全市征召義務宣傳志愿者，現從符合條件的500名志愿者中隨機抽取100名志愿者，他們的年齡情況如下表所示：
分組（單位：歲） | 頻數 | 頻率 |
| 5 | 0.05 |
| ① | 0.20 |
| 35 | ② |
| 30 | 0.30 |
| 10 | 0.10 |
總計 | 100 | 1.00 |
（1）頻率分布表中的①②位置應填什么數據？
（2）補全如圖所示的頻率分布直方圖，再根據頻率分布直方圖估計這500名志愿者中年齡在
歲的人數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在全國第五個“扶貧日”到來之前,某省開展“精準扶貧,攜手同行”的主題活動,某貧困縣調查基層干部走訪貧困戶數量．
鎮有基層干部60人,
鎮有基層干部60人,
鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從
三鎮共選40名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成5組,
,繪制成如圖所示的頻率分布直方圖．
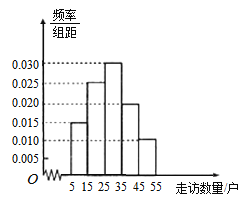
(1)求這40人中有多少人來自鎮,并估計三鎮的基層干部平均每人走訪多少貧困戶；(同一組中的數據用該組區間的中點值作代表)
(2)如果把走訪貧困戶達到或超過25戶視為工作出色,以頻率估計概率,從三鎮的所有基層干部中隨機選取3人,記這3人中工作出色的人數為
,求的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率是
，過點
作斜率為
的直線
交橢圓
于
兩點，當直線垂直于
軸時，
．
（1）求橢圓的方程
（2）當變化時，在
軸上是否存在點
，使得
是以
為底的等腰三角形？若存在，求出
的取值范圍；若不存在，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
