
若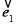 ,
,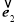 ,
,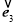 為同一平面內互不共線的三個單位向量,并滿足
為同一平面內互不共線的三個單位向量,并滿足 +
+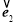 +
+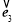 =
=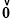 ,且向量
,且向量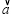 =x
=x +
+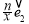 +(x+
+(x+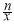 )
)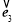 (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求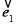 與
與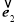 所成角的大小;
所成角的大小;
(2)記f(x)=|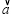 |,試求f(x)的單調區間及最小值.
|,試求f(x)的單調區間及最小值.
(1)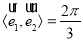 ;
;
(2)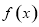 的減區間為
的減區間為 和
和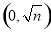 ;再由均值不等式易求得:
;再由均值不等式易求得: 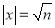 時,
時,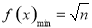 .
.
【解析】
試題分析:(1)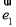 與
與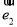 所成角的大小,首先求出向量
所成角的大小,首先求出向量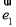 與
與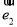 的數量積,由已知
的數量積,由已知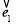 +
+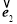 +
+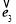 =
=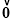 ,可得
,可得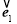 +
+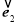 =-
=-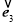 ,兩邊平方可得
,兩邊平方可得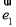 與
與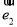 的數量積,再利用函數的數量積求出向量的夾角.(2)求
的數量積,再利用函數的數量積求出向量的夾角.(2)求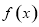 的單調區間及最小值,首先把向量的模長轉化為求向量的數量積,得函數
的單調區間及最小值,首先把向量的模長轉化為求向量的數量積,得函數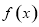 的解析式,進一步利用導數求出單調區間,最后確定最值.
的解析式,進一步利用導數求出單調區間,最后確定最值.
試題解析:(1)依題設:|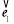 |=|
|=|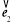 |=|
|=|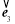 |=1,且
|=1,且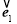 +
+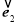 =-
=-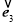 ⇒ (
⇒ (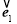 +
+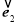 )2=(-
)2=(-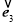 )2,化簡得:
)2,化簡得:
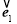 ·
·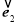 =-
=-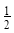 ⇒ cos<
⇒ cos<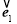 ,
,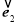 >=-
>=-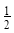 ,又<
,又<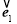 ,
,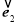 >∈[0, π] ⇒ <
>∈[0, π] ⇒ <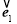 ,
,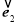 >=
>=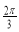 .
.
(2)由 (1)易知: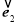 ·
·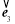 =
=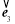 ·
·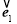 =
=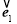 ·
·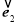 =-
=-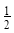 ,故由f(x)=|
,故由f(x)=| |=
|=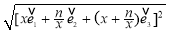 ,將其展開整理得: f(x)=
,將其展開整理得: f(x)=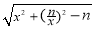 (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
①x>0時,對u(x)=x2+(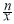 )2-n,求導并整理得:
)2-n,求導并整理得: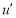 (x)=
(x)= .則由
.則由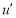 (x)>0⇒x>
(x)>0⇒x> ,且由
,且由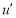 (x)<0⇒0<x<
(x)<0⇒0<x< .即f(x)的增區間為(
.即f(x)的增區間為( , +∞),減區間為(0,
, +∞),減區間為(0,  ).
).
②x<0時,因f(x)為偶函數,由圖像的對稱性知:f(x)的增區間為(- ,0),減區間為(-∞,-
,0),減區間為(-∞,- ).
).
綜上:f(x)的增區間為 (- ,0) 與 (
,0) 與 ( , +∞),f(x)的減區間為(-∞, -
, +∞),f(x)的減區間為(-∞, - ) 和 (0,
) 和 (0,  ).
).
再由均值不等式易求得:|x|= 時, f(x)min=
時, f(x)min= .
.
考點:向量的數量積,向量的夾角,向量的模,均值不等式,利用導數求函數的單調區間和最值.


科目:高中數學 來源:2015屆河北省石家莊市五校聯合體高三上學期第一次月考理科數學試卷(解析版) 題型:選擇題
若各項均為正數的等比數列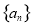 滿足
滿足 其前
其前 項的和為
項的和為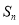 ,則
,則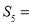 ( )
( )
A.31 B.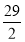 C.
C.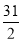 D.以上都不對
D.以上都不對
查看答案和解析>>
科目:高中數學 來源:2015屆河北省唐山市高三10月月考理科數學試卷(解析版) 題型:選擇題
使函數f(x)=sin(2x+θ)+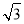 cos(2x+θ)是奇函數,且在區間
cos(2x+θ)是奇函數,且在區間 上是減函數的θ的一個值是 ( )
上是減函數的θ的一個值是 ( )
A.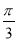 B.
B.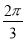 C.
C.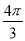 D.
D.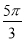
查看答案和解析>>
科目:高中數學 來源:2015屆江西省紅色六校高三第一次聯考文科數學試卷(解析版) 題型:選擇題
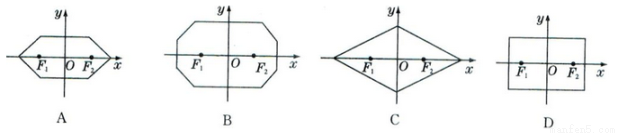
在平面直角坐標系中,兩點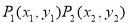 間的“L-距離”定義為
間的“L-距離”定義為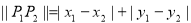 ,則平面內與
,則平面內與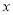 軸上兩個不同的定點
軸上兩個不同的定點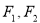 的“L-距離”之和等于定值(大于
的“L-距離”之和等于定值(大于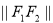 )的點的軌跡可以是( )
)的點的軌跡可以是( )
查看答案和解析>>
科目:高中數學 來源:2015屆江西省紅色六校高三第一次聯考文科數學試卷(解析版) 題型:選擇題
隨機擲兩枚質地均勻的骰子,它們向上的點數之和不超過4的概率記為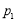 ,點數之和大于8的概率記為
,點數之和大于8的概率記為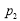 ,點數之和為奇數的概率記為
,點數之和為奇數的概率記為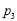 ,則 ( )
,則 ( )
A.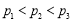 B.
B.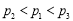
C.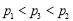 D.
D.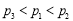
查看答案和解析>>
科目:高中數學 來源:2015屆江西省南昌市三校高三10月聯考理科數學試卷(解析版) 題型:填空題
若等腰△ABC底邊BC上的中線長為1,底角B>60º,則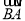 ·
·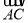 的取值范圍是______.
的取值范圍是______.
查看答案和解析>>
科目:高中數學 來源:2015屆江西省南昌市三校高三10月聯考理科數學試卷(解析版) 題型:選擇題
已知 ,
, 是不共線的向量,若
是不共線的向量,若 =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),則A, B, C三點共線的充要條件是:( )
(λ,μ∈R),則A, B, C三點共線的充要條件是:( )
A.λ+μ=1 B.λ-μ=1 C.λμ=1 D.λμ=-1
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇省連云港高二下學期期末數學試卷(選修物理)(解析版) 題型:填空題
將1、2、3、4、5、6、7、8、9這9個正整數分別寫在三張卡片上,要求每一張卡片上的三個數字中任意兩數之差都不在這張卡片上.現在第一張卡片上已經寫有1和5,第二張卡片上寫有2,第三張卡片上寫有3,則第一張卡片上的另外一個數字是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com