【題目】如圖是函數
的導函數
的圖象，給出下列命題：
①-2是函數的極值點；
②1是函數的極值點；
③的圖象在
處切線的斜率小于零；
④函數在區間
上單調遞增.
則正確命題的序號是（ ）
A. ①③ B. ②④ C. ②③ D. ①④
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中,已知傾斜角為
的直線
經過點
.以坐標原點
為極點,
軸的正半軸為極軸建立極坐標系,曲線
的極坐標方程為
(1)寫出曲線的普通方程;
(2)若直線與曲線有兩個不同的交點
,求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地隨著經濟的發展，居民收入逐年增長，下表是該地一建設銀行連續五年的儲蓄存款（年底余額），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y （千億元） | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便，工作人員將上表的數據進行了處理，
得到下表2：
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（1）求z關于t的線性回歸方程；
（2）通過（1）中的方程，求出y關于x的回歸方程；
（3）用所求回歸方程預測到2020年年底，該地儲蓄存款額可達多少？
（附：對于線性回歸方程
，其中
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，點列{An}、{Bn}分別在銳角兩邊（不在銳角頂點），且|AnAn+1|=|An+1An+2|，An≠An+2 ， |BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+1 ， n∈N*（P≠Q表示點P與Q不重合），若dn=|AnBn|，Sn為△AnBnBn+1的面積，則（ ） 
A.{dn}是等差數列
B.{Sn}是等差數列
C.{d 
}是等差數列
D.{S }是等差數列
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}的前n項和記為Sn且滿足Sn=2an﹣1，n∈N*；
（1）求數列{an}的通項公式；
（2）設Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+（﹣1）n+1anan+1 ， 求{Tn}的通項公式；
（3）設有m項的數列{bn}是連續的正整數數列，并且滿足：lg2+lg（1+ 
）+lg（1+ 
）+…+lg（1+ 
）=lg（log2am）．
問數列{bn}最多有幾項？并求出這些項的和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
右焦點
，離心率為
，過
作兩條互相垂直的弦
，設
中點分別為
.
（1）求橢圓的方程；
(2) 證明：直線
必過定點，并求出此定點坐標；
(3) 若弦
的斜率均存在，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形
中，
，
，
，將四邊形沿對角線
折成四面
．使平面
平面
，則下列結論正確的是（ ）．
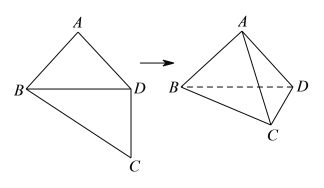
A. 
B. 
C. 
與平面
所成的角為
D. 四面體的體積為
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
