
分析 (Ⅰ)利用函數g(x)=k(x)-$\frac{1}{2}x$為偶函數,結合k(-1)=0,求出a,b,c,即可求函數k(x)的表達式;
(Ⅱ)求出0$<\frac{{x}_{1}}{{x}_{2}}≤\frac{1}{2}$,y=(x1-x2)φ′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$-$ln\frac{{x}_{1}}{{x}_{2}}$,再換元,構造函數,求導數,確定函數的單調性,求出函數的最小值,即可得出結論.
解答 解:(Ⅰ)由已知可得k(x)=ax2+bx+c.
∵函數g(x)=k(x)-$\frac{1}{2}x$為偶函數,
∴ax2-bx+c+$\frac{1}{2}$x=ax2+bx+c-$\frac{1}{2}x$,
∴(a-$\frac{1}{2}$)x2+$\frac{1}{2}x$+c-$\frac{1}{2}$≤0恒成立,
∴$\left\{\begin{array}{l}{a-\frac{1}{2}<0}\\{\frac{1}{4}-4(a-\frac{1}{2})(c-\frac{1}{2})≤0}\end{array}\right.$
∴a=c=$\frac{1}{4}$.
∵k(-1)=0,∴得k(x)=$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{1}{4}$.
(Ⅱ)由(Ⅰ)得,f(x)=$\frac{1}{12}{x}^{3}$+$\frac{1}{4}$x2+$\frac{1}{4}$x.
∴h(x)=2lnx+x2+3-2mx,
∴h′(x)=$\frac{2({x}^{2}-mx+1)}{x}$.
由題意得△=m2-4>0,x1+x2=m,x1x2=1
又m$≥\frac{3\sqrt{2}}{2}$,
∴解得0$<\frac{{x}_{1}}{{x}_{2}}≤\frac{1}{2}$.
∵x1,x2(x1<x2)恰為φ(x)=lnx-sx2-tx的零點,
∴代入,兩式相減得,$ln\frac{{x}_{1}}{{x}_{2}}$-s(x1-x2)(x1+x2)-t(x1-x2)=0.
又φ′(x)=$\frac{1}{x}$-2sx-t,從而y=(x1-x2)φ′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$-$ln\frac{{x}_{1}}{{x}_{2}}$.
設n=$\frac{{x}_{1}}{{x}_{2}}$(0$<n≤\frac{1}{2}$),
則y=(x1-x2)φ′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{2(n-1)}{n+1}$-lnn(0$<n≤\frac{1}{2}$),記為M(n).
M′(n)=$\frac{-(n-1)^{2}}{n(n+1)^{2}}$<0
∴M(n)在(0,$\frac{1}{2}$]上單調遞減.
∴M(n)min=ln2-$\frac{2}{3}$.
故y=(x1-x2)φ′($\frac{{x}_{1}+{x}_{2}}{2}$)的最小值為ln2-$\frac{2}{3}$.
點評 本題考查導數知識的綜合運用,考查函數的性質,考查構造函數方法的運用,難度大.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 2 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{n+1}{2(n+2)}$ | B. | $\frac{3}{4}$-$\frac{n+1}{2(n+2)}$ | C. | $\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$) | D. | $\frac{3}{2}$-$\frac{1}{n+1}$+$\frac{1}{n+2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
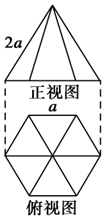 如圖是一個幾何體的正視圖和俯視圖.
如圖是一個幾何體的正視圖和俯視圖.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com