
定義函數(shù)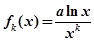 為
為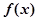 的
的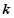 階函數(shù).
階函數(shù).
(1)求一階函數(shù)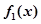 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)討論方程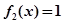 的解的個(gè)數(shù);
的解的個(gè)數(shù);
(3)求證: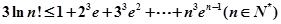 .
.
(1)當(dāng)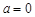 時(shí),
時(shí),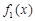 無單調(diào)區(qū)間;
無單調(diào)區(qū)間;
當(dāng)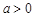 時(shí),
時(shí),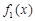 的單增區(qū)間為
的單增區(qū)間為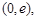 單減區(qū)間為
單減區(qū)間為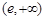 ;
;
當(dāng)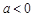 時(shí),
時(shí),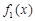 的單增區(qū)間為
的單增區(qū)間為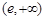 ,單減區(qū)間為
,單減區(qū)間為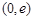 ;
;
(2)當(dāng)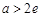 時(shí),方程有兩個(gè)不同解.當(dāng)
時(shí),方程有兩個(gè)不同解.當(dāng)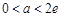 時(shí),方程有0個(gè)解.當(dāng)
時(shí),方程有0個(gè)解.當(dāng)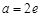 或
或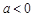 時(shí),方程有唯一;
時(shí),方程有唯一;
(3)詳見解析.
【解析】
試題分析:(1)求導(dǎo),對(duì)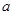 分情況討論;
分情況討論;
(2)研究方程的解的個(gè)數(shù),實(shí)質(zhì)就是研究函數(shù)的圖象.通過求導(dǎo),弄清函數(shù)的單調(diào)區(qū)間及函數(shù)值的范圍,結(jié)合圖象即可知道方程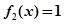 的解的個(gè)數(shù).
的解的個(gè)數(shù).
(3)待證不等式 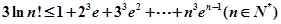
可變?yōu)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014030605172678714283/SYS201403060521285058540406_DA.files/image014.png">,左右對(duì)照,考慮證:
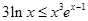
再聯(lián)系到本題所給函數(shù),可令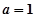 ,且研究
,且研究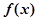 的3階函數(shù),即
的3階函數(shù),即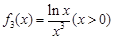 .
.
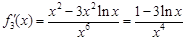 .由
.由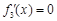 得
得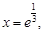
則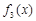 在
在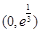 單調(diào)遞增,在
單調(diào)遞增,在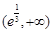 單調(diào)遞減.
單調(diào)遞減.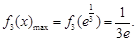
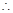
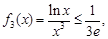 即
即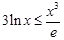 .又
.又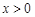 時(shí),
時(shí),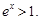
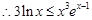
再令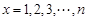 即得證.
即得證.
令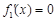 ,當(dāng)
,當(dāng)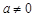 時(shí),
時(shí),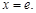
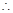 當(dāng)
當(dāng)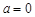 時(shí),
時(shí),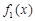 無單調(diào)區(qū)間;
無單調(diào)區(qū)間;
當(dāng)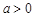 時(shí),
時(shí),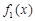 的單增區(qū)間為
的單增區(qū)間為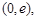 單減區(qū)間為
單減區(qū)間為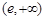 .
.
當(dāng)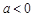 時(shí),
時(shí),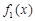 的單增區(qū)間為
的單增區(qū)間為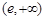 ,單減區(qū)間為
,單減區(qū)間為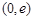 .
.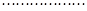 4分.
4分.
(2)由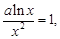 當(dāng)
當(dāng)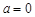 時(shí),方程無解.當(dāng)
時(shí),方程無解.當(dāng)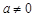 時(shí),
時(shí),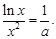
令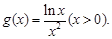 則
則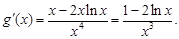 由
由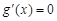 得
得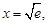
從而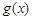 在
在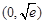 單調(diào)遞增,在
單調(diào)遞增,在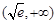 單調(diào)遞減.
單調(diào)遞減.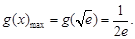
當(dāng)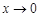 時(shí),
時(shí),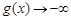 ,當(dāng)
,當(dāng)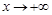
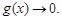
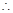 當(dāng)
當(dāng)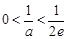 ,即
,即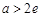 時(shí),方程有兩個(gè)不同解.
時(shí),方程有兩個(gè)不同解.
當(dāng)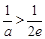 ,即
,即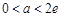 時(shí),方程有0個(gè)解
時(shí),方程有0個(gè)解
當(dāng)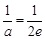 ,
,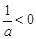 或即
或即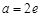 或
或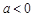 時(shí),方程有唯一解.
時(shí),方程有唯一解.
綜上,當(dāng)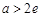 時(shí),方程有兩個(gè)不同解.當(dāng)
時(shí),方程有兩個(gè)不同解.當(dāng)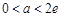 時(shí),方程有0個(gè)解.當(dāng)
時(shí),方程有0個(gè)解.當(dāng)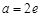 或
或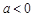 時(shí),方程有唯一解. 9分.
時(shí),方程有唯一解. 9分.
(3)特別地:當(dāng)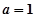 時(shí)由
時(shí)由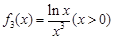 得
得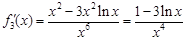 .
.
由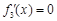 得
得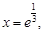
則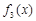 在
在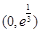 單調(diào)遞增,在
單調(diào)遞增,在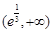 單調(diào)遞減.
單調(diào)遞減.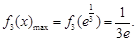
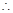
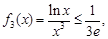 即
即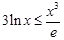 .又
.又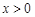 時(shí),
時(shí),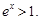
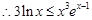 12分.
12分.
令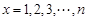 ,
,
則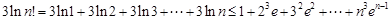 14分.
14分.
考點(diǎn):1、導(dǎo)數(shù)的應(yīng)用;2、不等式的證明.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年四川成都七中高三“一診”模擬考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
定義函數(shù)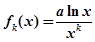 為
為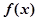 的
的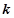 階函數(shù).
階函數(shù).
(1)求一階函數(shù)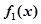 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)討論方程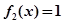 的解的個(gè)數(shù);
的解的個(gè)數(shù);
(3)求證: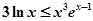 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西新余第一中學(xué)高三第七次模擬考試文科數(shù)學(xué)試卷(解析版) 題型:填空題
對(duì)于定義域和值域均為 的函數(shù)
的函數(shù)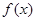 ,定義
,定義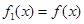 ,
,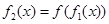 ,…,
,…,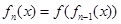 ,n=1,2,3,….滿足
,n=1,2,3,….滿足 的點(diǎn)稱為f的
的點(diǎn)稱為f的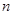 階周期點(diǎn).
階周期點(diǎn).
(1)設(shè)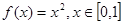 則f的
則f的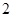 階周期點(diǎn)的個(gè)數(shù)是___________;
階周期點(diǎn)的個(gè)數(shù)是___________;
(2)設(shè)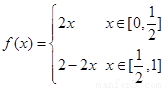 則f的
則f的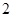 階周期點(diǎn)的個(gè)數(shù)是__________ .
階周期點(diǎn)的個(gè)數(shù)是__________ .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年四川省高三2月月考數(shù)學(xué)理卷 題型:解答題
(本小題14分)
已知函數(shù)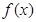 的圖像在[a,b]上連續(xù)不斷,定義:
的圖像在[a,b]上連續(xù)不斷,定義:
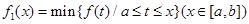 ,
, ,其中
,其中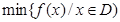 表示函數(shù)
表示函數(shù)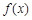 在D上的最小值,
在D上的最小值, 表示函數(shù)
表示函數(shù)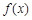 在D上的最大值,若存在最小正整數(shù)k,使得
在D上的最大值,若存在最小正整數(shù)k,使得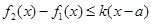 對(duì)任意的
對(duì)任意的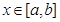 成立,則稱函數(shù)
成立,則稱函數(shù)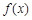 為
為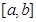 上的“k階收縮函數(shù)”
上的“k階收縮函數(shù)”
(1)若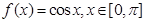 ,試寫出
,試寫出 ,
,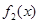 的表達(dá)式;
的表達(dá)式;
(2)已知函數(shù)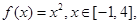 試判斷
試判斷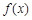 是否為[-1,4]上的“k階收縮函數(shù)”,
是否為[-1,4]上的“k階收縮函數(shù)”,
如果是,求出對(duì)應(yīng)的k,如果不是,請(qǐng)說明理由;
已知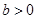 ,函數(shù)
,函數(shù)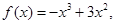 是[0,b]上的2階收縮函數(shù),求b的取值范圍
是[0,b]上的2階收縮函數(shù),求b的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年四川省高三2月月考數(shù)學(xué)理卷 題型:解答題
(本小題14分)
已知函數(shù) 的圖像在[a,b]上連續(xù)不斷,定義:
的圖像在[a,b]上連續(xù)不斷,定義:
 ,
, ,其中
,其中 表示函數(shù)
表示函數(shù) 在D上的最小值,
在D上的最小值, 表示函數(shù)
表示函數(shù) 在D上的最大值,若存在最小正整數(shù)k,使得
在D上的最大值,若存在最小正整數(shù)k,使得 對(duì)任意的
對(duì)任意的 成立,則稱函數(shù)
成立,則稱函數(shù) 為
為 上的“k階收縮函數(shù)”
上的“k階收縮函數(shù)”
(1)若 ,試寫出
,試寫出 ,
, 的表達(dá)式;
的表達(dá)式;
(2)已知函數(shù) 試判斷
試判斷 是否為[-1,4]上的“k階收縮函數(shù)”,
是否為[-1,4]上的“k階收縮函數(shù)”,
如果是,求出對(duì)應(yīng)的k,如果不是,請(qǐng)說明理由;
已知 ,函數(shù)
,函數(shù) 是[0,b]上的2階收縮函數(shù),求b的取值范圍
是[0,b]上的2階收縮函數(shù),求b的取值范圍
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com