
(本小題滿分l3分)
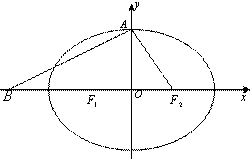
設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為
,上頂點為![]() ,在
,在![]() 軸負半軸上有一點
軸負半軸上有一點![]() ,滿足
,滿足![]() ,且
,且![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)若過![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() 相切,求橢圓
相切,求橢圓![]() 的方程;
的方程;
 (3)在(2)的條件下,過右焦點
(3)在(2)的條件下,過右焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() 為鄰邊的平行四邊形是菱形,如果存在,求出
為鄰邊的平行四邊形是菱形,如果存在,求出![]() 的取值范圍,如果不存在,說明理由。
的取值范圍,如果不存在,說明理由。
科目:高中數學 來源:2010年福州市八縣(市)協作校高二第二學期期末聯考數學(理)試卷 題型:解答題
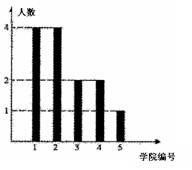
(本小題滿分12分)上海世博會舉辦時間為2010年5月1日~10月31日。福建館以“海西”為參博核心元素,主題為“潮涌海西,魅力福建”。福建館招募了60名志愿者,某高校有l3人入選,其中5人為中英文講解員,8人為迎賓禮儀,它們來自該校的5所所學院(這5所學院編號為1~5號),人員分布如圖所示。若從這13名入選者中隨機抽取3人。
(1)求這3人所在學院的編號恰好成等比數列的概率;
(2)求這3人中中英文講解員人數的分布列及數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分l3分)
設橢圓![]() 的焦點分別為
的焦點分別為![]() 、
、![]() ,直線
,直線![]() :
:![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() .
.
(1)試求橢圓的方程;
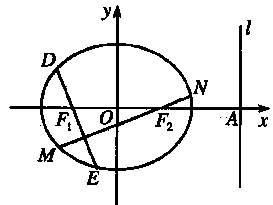
(2)過![]() 、
、![]() 分別作互相垂直的兩直線與橢圓分別交于
分別作互相垂直的兩直線與橢圓分別交于![]() 、
、![]() 、
、![]() 、
、![]() 四點(如圖所示),試求四邊形
四點(如圖所示),試求四邊形![]() 面積的最大值和最小值.
面積的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分l3分)
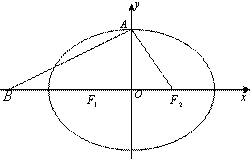
設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為
,上頂點為![]() ,在
,在![]() 軸負半軸上有一點
軸負半軸上有一點![]() ,滿足
,滿足![]() ,且
,且![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)若過![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() 相切,求橢圓
相切,求橢圓![]() 的方程;
的方程;
 (3)在(2)的條件下,過右焦點
(3)在(2)的條件下,過右焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() 為鄰邊的平行四邊形是菱形,如果存在,求出
為鄰邊的平行四邊形是菱形,如果存在,求出![]() 的取值范圍,如果不存在,說明理由。
的取值范圍,如果不存在,說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com