
【題目】設(shè)函數(shù)![]() ,
,![]() ,其中
,其中![]() ,
,![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)若![]() 在
在![]() 上存在兩個極值點,求
上存在兩個極值點,求![]() 的取值范圍;
的取值范圍;
(2)若![]() ,
,![]() ,函數(shù)
,函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖象交于
的圖象交于![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 線段的中點為
線段的中點為![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;;(2)見解析.
;;(2)見解析.
【解析】
(1)求導(dǎo),依題意,導(dǎo)函數(shù)滿足![]() 在
在![]() 上有兩個不等實根,轉(zhuǎn)化可得
上有兩個不等實根,轉(zhuǎn)化可得![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)可知
,利用導(dǎo)數(shù)可知![]() ,且由
,且由![]() 的趨近性可求得實數(shù)
的趨近性可求得實數(shù)![]() 的取值范圍;
的取值范圍;
(2)問題轉(zhuǎn)化為證明![]() ,通過換元令
,通過換元令![]() ,即證
,即證![]() ,再分別證明即可.
,再分別證明即可.
(1)由題意可知,![]() ,令
,令![]() ,
,
則![]() 在
在![]() 上存在兩個極值點等價于
上存在兩個極值點等價于![]() 在
在![]() 上有兩個不等實根,
上有兩個不等實根,
由![]() 可得
可得![]() ,
,
令![]() ,則
,則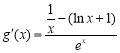 ,
,
令![]() ,則
,則![]() ,
,
當(dāng)![]() 時,
時,![]() ,故函數(shù)
,故函數(shù)![]() 在
在![]() 上單調(diào)遞減,且
上單調(diào)遞減,且![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時,
時,![]() ,
,![]() ,
,![]() 單調(diào)遞增,
單調(diào)遞增,
當(dāng)![]() 時,
時,![]() ,
,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
![]() 是
是![]() 的極大值也是最大值,
的極大值也是最大值,
![]()
![]() ,
,
![]()
![]() ,
,
又當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() 大于0且趨向于0,
大于0且趨向于0,
要使![]() 在
在![]() 有兩個根,則
有兩個根,則![]() ;
;
(2)由題意可得![]() ,
,![]() ,
,
要證![]() (1)
(1)![]() 成立,
成立,
只需證![]() ,即
,即![]() ,
,
設(shè)![]() ,即證
,即證![]() ,
,
要證![]() ,只需證
,只需證![]() ,
,
令![]() ,則
,則![]() ,
,
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
![]() ,即
,即![]() 成立;
成立;
要證![]() ,只需證
,只需證![]() ,
,
令![]() ,則
,則![]() ,
,
![]() 在
在![]() 上為減函數(shù),
上為減函數(shù),
![]() ,即
,即![]() 成立;
成立;
![]()
![]() 成立,
成立,
即![]() 成立.
成立.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a,b,c為正實數(shù),且滿足a+b+c=1.證明:
(1)|a![]() |+|b+c﹣1|
|+|b+c﹣1|![]() ;
;
(2)(a3+b3+c3)(![]() )≥3.
)≥3.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年3月12日,國務(wù)院新聞辦公室發(fā)布會重點介紹了改革開放40年,特別是黨的十八大以來我國脫貧攻堅、精準(zhǔn)扶貧取得的顯著成績,這些成績?yōu)槿婷撠毘醪浇ǔ尚】瞪鐣於藞詫嵉幕A(chǔ).下圖是統(tǒng)計局公布的2010年~2019年年底的貧困人口和貧困發(fā)生率統(tǒng)計表.則下面結(jié)論正確的是( )
(年底貧困人口的線性回歸方程為![]() (其中
(其中![]() 年份-2019),貧困發(fā)生率的線性回歸方程為
年份-2019),貧困發(fā)生率的線性回歸方程為![]() (其中
(其中![]() 年份-2009))
年份-2009))

A.2010年~2019年十年間脫貧人口逐年減少,貧困發(fā)生率逐年下降
B.2012年~2019年連續(xù)八年每年減貧超過1000萬,且2019年貧困發(fā)生率最低
C.2010年~2019年十年間超過1.65億人脫貧,其中2015年貧困發(fā)生率低于6%
D.根據(jù)圖中趨勢線可以預(yù)測,到2020年底我國將實現(xiàn)全面脫貧
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,四點
,四點![]() ,
,![]() ,
,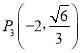 ,
,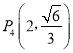 中恰有三個點在橢圓C上,左、右焦點分別為F1、F2.
中恰有三個點在橢圓C上,左、右焦點分別為F1、F2.
(1)求橢圓C的方程;
(2)過左焦點F1且不平行坐標(biāo)軸的直線l交橢圓于P、Q兩點,若PQ的中點為N,O為原點,直線ON交直線x=﹣3于點M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,其中
,其中![]() ,
,![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)若![]() 在
在![]() 上存在兩個極值點,求
上存在兩個極值點,求![]() 的取值范圍;
的取值范圍;
(2)若![]() ,
,![]() ,函數(shù)
,函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖象交于
的圖象交于![]() ,
,![]() ,且
,且![]() 線段的中點為
線段的中點為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 的極小值點,求實數(shù)a的取值范圍。
的極小值點,求實數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】法國數(shù)學(xué)家龐加是個喜歡吃面包的人,他每天都會購買一個面包,面包師聲稱自己出售的每個面包的平均質(zhì)量是1000![]() ,上下浮動不超過50
,上下浮動不超過50![]() .這句話用數(shù)學(xué)語言來表達(dá)就是:每個面包的質(zhì)量服從期望為1000
.這句話用數(shù)學(xué)語言來表達(dá)就是:每個面包的質(zhì)量服從期望為1000![]() ,標(biāo)準(zhǔn)差為50
,標(biāo)準(zhǔn)差為50![]() 的正態(tài)分布.
的正態(tài)分布.
(1)假設(shè)面包師的說法是真實的,從面包師出售的面包中任取兩個,記取出的兩個面包中質(zhì)量大于1000![]() 的個數(shù)為
的個數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(2)作為一個善于思考的數(shù)學(xué)家,龐加萊每天都會將買來的面包稱重并記錄,25天后,得到數(shù)據(jù)如下表,經(jīng)計算25個面包總質(zhì)量為24468![]() .龐加萊購買的25個面包質(zhì)量的統(tǒng)計數(shù)據(jù)(單位:
.龐加萊購買的25個面包質(zhì)量的統(tǒng)計數(shù)據(jù)(單位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
盡管上述數(shù)據(jù)都落在![]() 上,但龐加菜還是認(rèn)為面包師撒謊,根據(jù)所附信息,從概率角度說明理由
上,但龐加菜還是認(rèn)為面包師撒謊,根據(jù)所附信息,從概率角度說明理由
附:
①若![]() ,從X的取值中隨機(jī)抽取25個數(shù)據(jù),記這25個數(shù)據(jù)的平均值為Y,則由統(tǒng)計學(xué)知識可知:隨機(jī)變量
,從X的取值中隨機(jī)抽取25個數(shù)據(jù),記這25個數(shù)據(jù)的平均值為Y,則由統(tǒng)計學(xué)知識可知:隨機(jī)變量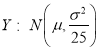
②若![]() ,則
,則![]() ,
,![]() ,
,![]() ;
;
③通常把發(fā)生概率在0.05以下的事件稱為小概率事件.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為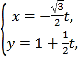 (
(![]() 為參數(shù)),以原點為極點,
為參數(shù)),以原點為極點, ![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的方程為
的方程為![]() ,定點
,定點![]() ,點
,點![]() 是曲線
是曲線![]() 上的動點,
上的動點, ![]() 為
為![]() 的中點.
的中點.
(1)求點![]() 的軌跡
的軌跡![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,若
,若![]() 的中點為
的中點為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com