
��֪���タ ����c(di��n)������(bi��o)ԭ�c(di��n)
����c(di��n)������(bi��o)ԭ�c(di��n)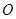 ����(du��)�Q�S��
����(du��)�Q�S�� �S�����c(di��n)��
�S�����c(di��n)��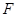 ,���タ��һ�c(di��n)
,���タ��һ�c(di��n)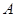 �ęM����(bi��o)��2����
�ęM����(bi��o)��2����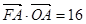 .
.
(1)���タ�ķ��̣�
(2)�^(gu��)�c(di��n)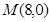 ��ֱ��
��ֱ�� �����タ��
�����タ��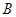 ��
�� ���c(di��n),���C:
���c(di��n),���C: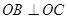 .
.
(1)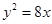 (2)ԔҊ(ji��n)����.
(2)ԔҊ(ji��n)����.
����ԇ�}������(1)�����ô���ϵ��(sh��)���O(sh��)���タ���̞�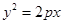
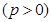 ��⣻
��⣻
(2)��?y��n)���ֱ���c�A�F�������ཻ��(w��n)�������O(sh��)ֱ�����̣�б�ʲ����ڕr(sh��)�Ϊ�(d��)ӑՓ����Ȼ��(li��n)�����タ���̺�ֱ�������\(y��n)���f�_(d��)�����Y(ji��)�ϗl����(l��i)���.
ԇ�}�������⣺(1)���}�O(sh��)���タ�ķ��̞飺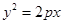
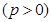 ��
��
�t�c(di��n)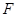 ������(bi��o)��
������(bi��o)��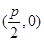 ���c(di��n)
���c(di��n)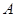 ��һ��(g��)����(bi��o)��
��һ��(g��)����(bi��o)��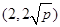 ��2��
��2��
��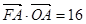 ����
����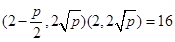 ��4��
��4��
��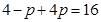 ����
����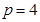 ����
����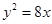 .6��
.6��
(2)�O(sh��)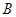 ��
�� ���c(di��n)����(bi��o)�քe��
���c(di��n)����(bi��o)�քe��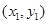 ��
�� ��
��
��һ����?y��n)�ֱ����(d��ng) ��б�ʲ���0���O(sh��)ֱ����(d��ng)
��б�ʲ���0���O(sh��)ֱ����(d��ng) �ķ��̞�
�ķ��̞�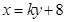
���̽M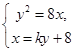 ��
�� ��
��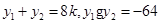
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/c6/7/nejhp1.png" style="vertical-align:middle;" />
����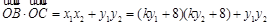
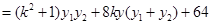 =0��
=0��
����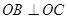 .
.
�������ٮ�(d��ng) ��б�ʲ����ڕr(sh��)��
��б�ʲ����ڕr(sh��)�� �ķ��̞�
�ķ��̞�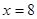 ���˕r(sh��)
���˕r(sh��)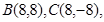
�� ��
��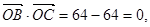 ����
����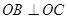 .���� 8��
.���� 8��
��(d��ng) ��б�ʴ��ڕr(sh��)���O(sh��)
��б�ʴ��ڕr(sh��)���O(sh��) �ķ��̞�
�ķ��̞�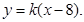
���̽M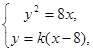 ��
��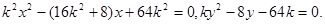
���� 10��
10��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/c6/7/nejhp1.png" style="vertical-align:middle;" />
����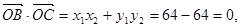
����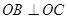 .
.
�ɢ٢ڵ�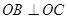 .12��
.12��
���c(di��n)��1.���タ�Ę�(bi��o)��(zh��n)���̣�2.ֱ���c�A�F������λ���P(gu��n)ϵ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�x���ʞ�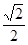 �ęE�A
�ęE�A (
( )�^(gu��)�c(di��n)
)�^(gu��)�c(di��n)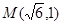
(1)��E�A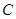 �ķ���;
�ķ���;
(2)�^(gu��)�c(di��n)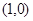 ��б�ʞ�
��б�ʞ�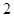 ֱ��
ֱ�� �c�E�A�ཻ��
�c�E�A�ཻ�� ���c(di��n)����
���c(di��n)���� ���L(zh��ng).
���L(zh��ng).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A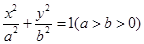 ���ҽ��c(di��n)��F2��1��0�����c(di��n)
���ҽ��c(di��n)��F2��1��0�����c(di��n)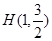 �ڙE�A��.
�ڙE�A��.
��1����E�A���̣�
��2���c(di��n)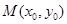 �ڈA
�ڈA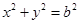 �ϣ�M�ڵ�һ���ޣ��^(gu��)M���A
�ϣ�M�ڵ�һ���ޣ��^(gu��)M���A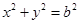 ���о����E�A��P��Q���c(di��n)����(w��n)|F2P|+|F2Q|+|PQ|�Ƿ�鶨ֵ������ǣ������ֵ���粻�ǣ��f(shu��)������.
���о����E�A��P��Q���c(di��n)����(w��n)|F2P|+|F2Q|+|PQ|�Ƿ�鶨ֵ������ǣ������ֵ���粻�ǣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)�E�A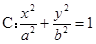
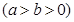 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)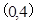 ���x���ʞ�
���x���ʞ�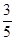 .
.
��1����E�A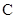 �ķ��̣�
�ķ��̣�
��2�����^(gu��)�c(di��n)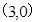 ��б�ʞ�
��б�ʞ�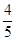 ��ֱ�����E�A���صþ��ε����c(di��n)����(bi��o).
��ֱ�����E�A���صþ��ε����c(di��n)����(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪������ԭ�c(di��n)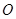 �ęE�AC��
�ęE�AC��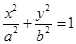 ��һ��(g��)���c(di��n)��F1(0,3)��M(x,4)(x��0)��E�AC��һ�c(di��n)����MOF1����e��
��һ��(g��)���c(di��n)��F1(0,3)��M(x,4)(x��0)��E�AC��һ�c(di��n)����MOF1����e��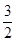 .
.
��1�� ��E�AC�ķ��̣�
��2�� �Ƿ����ƽ����OM��ֱ��l��ʹ��ֱ��l�c�E�AC�ཻ��A��B���c(di��n)�����Ծ���AB��ֱ���ĈAǡ�ý�(j��ng)�^(gu��)ԭ�c(di��n)�������ڣ����ֱ��l�ķ��̣��������ڣ��f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���タ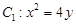 ���c(di��n)
���c(di��n)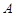 ��
��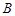 ̎���о���ֱ�ཻ���c(di��n)
̎���о���ֱ�ཻ���c(di��n) ��ֱ��
��ֱ��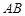 �c�E�A
�c�E�A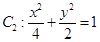 �ཻ��
�ཻ��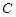 ��
��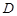 ���c(di��n)��
���c(di��n)��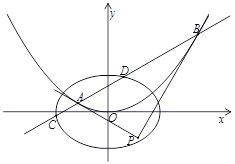
��1�����タ �Ľ��c(di��n)
�Ľ��c(di��n)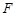 �c�E�A
�c�E�A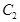 �����c(di��n)
�����c(di��n) �ľ��x��
�ľ��x��
��2���O(sh��)�c(di��n) ��ֱ��
��ֱ��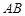 �ľ��x��
�ľ��x��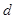 ��ԇ��(w��n)���Ƿ����ֱ��
��ԇ��(w��n)���Ƿ����ֱ��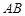 ��ʹ��
��ʹ��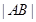 ��
��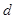 ��
��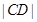 �ɵȱȔ�(sh��)�У������ڣ���ֱ��
�ɵȱȔ�(sh��)�У������ڣ���ֱ��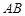 �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���ԙE�A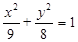 �Ľ��c(di��n)�齹�c(di��n)�����^(gu��)
�Ľ��c(di��n)�齹�c(di��n)�����^(gu��)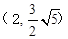 �c(di��n)���p�����Ę�(bi��o)��(zh��n)����.
�c(di��n)���p������(bi��o)��(zh��n)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���タ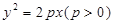 �����(zh��n)�����̞�
�����(zh��n)�����̞�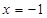 ���^(gu��)��(zh��n)���c
���^(gu��)��(zh��n)���c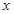 �S�Ľ��c(di��n)
�S�Ľ��c(di��n)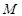 ��ֱ��
��ֱ��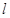 �����タ��
�����タ�� ���c(di��n).
���c(di��n).
��1�����c(di��n)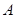 ��
��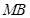 ���c(di��n)����ֱ��
���c(di��n)����ֱ��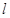 �ķ��̣�
�ķ��̣�
��2���O(sh��)���タ�Ľ��c(di��n)��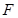 ����(d��ng)
����(d��ng)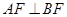 �r(sh��)����
�r(sh��)����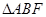 ����e��
����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ�У���֪�c(di��n)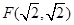 ��ֱ��
��ֱ��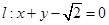 ������
������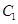 �ǝM�����Ѓɂ�(g��)�l���Ą�(d��ng)�c(di��n)
�ǝM�����Ѓɂ�(g��)�l���Ą�(d��ng)�c(di��n)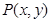 ��܉�E����
��܉�E����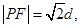 ����
����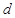 ��
��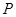 ��ֱ��
��ֱ��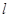 �ľ��x����
�ľ��x����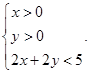
(1) ������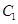 �ķ���;
�ķ���;
(2) ������ֱ��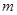 �c����
�c����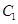 ���E�A
���E�A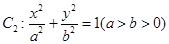 ��������ͬһ�c(di��n)����E�A
��������ͬһ�c(di��n)����E�A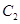 �x����
�x����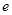 ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com