
【題目】已知向量 ![]() 與向量
與向量 ![]() 的夾角為θ,且|
的夾角為θ,且| ![]() |=1,|
|=1,| ![]() |=
|= ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]()
![]() ;
;
(2)若 ![]() ﹣
﹣ ![]() 與
與 ![]() 垂直,求θ.
垂直,求θ.
 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)求f(f( ![]() ));
));
(2)若x0滿足f(f(x0))=x0 , 且f(x0)≠x0 , 則稱x0為f(x)的二階不動點,求函數f(x)的二階不動點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,PD=AD=AB=1,DC=2. 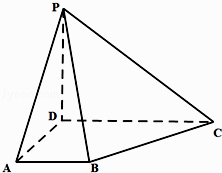
(1)求證:BC⊥平面PBD;
(2)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體,它的正視圖為直角三角形,側視圖為正三角形,俯視圖為正方形(尺寸如圖所示),E為VB的中點. 
(1)求證:VD∥平面EAC;
(2)求二面角A﹣VB﹣D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線E的中心為原點,P(3,0)是E的焦點,過P的直線l與E相交于A,B兩點,且AB的中點為N(﹣12,﹣15),則E的方程式為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,銳角α和鈍角β的終邊分別與單位圓交于A,B兩點. 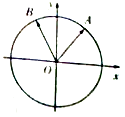
(I)若A,B兩點的縱會標分別為 ![]() 的值;
的值;
(II)已知點C是單位圓上的一點,且 ![]() 的夾角θ.
的夾角θ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,F1、F2是雙曲線 ![]() =1(a>0,b>0)的左、右焦點,過F1的直線l與雙曲線的左右兩支分別交于點A、B.若△ABF2為等邊三角形,則雙曲線的離心率為( )
=1(a>0,b>0)的左、右焦點,過F1的直線l與雙曲線的左右兩支分別交于點A、B.若△ABF2為等邊三角形,則雙曲線的離心率為( ) 
A.4
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的方程為:ax2+ay2﹣2a2x﹣4y=0(a≠0,a為常數).
(1)判斷曲線C的形狀;
(2)設曲線C分別與x軸、y軸交于點A、B(A、B不同于原點O),試判斷△AOB的面積S是否為定值?并證明你的判斷;
(3)設直線l:y=﹣2x+4與曲線C交于不同的兩點M、N,且|OM|=|ON|,求曲線C的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com