Question

已知集合A={（x，y）|x²+mx-y+2=0}和B={（x，y）|x-y+1=0，0≤x≤2}，A∩B≠∅，求實數m的
取值范圍．

Answer 1

【答案】分析：本題的幾何背景是：拋物線y=x²+mx+2與線段y=x+1（0≤x≤2）有公共點，求實數m的取值范圍．
解答：解：由
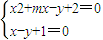
得x²+（m-1）x+1=0，①
∵A∩B≠∅，
∴方程①在區間[0，2]上至少有一個實數解，
首先，由△=（m-1）²-4≥0，
解得：m≥3或m≤-1．
設方程①的兩個根為x₁、x₂，
（1）當m≥3時，由x₁+x₂=-（m-1）＜0
及x₁•x₂=1＞0知x₁、x₂都是負數，不合題意；
（2）當m≤-1時，由x₁+x₂=-（m-1）＞0
及x₁•x₂=1＞0知x₁、x₂是互為倒數的兩個正數，
故x₁、x₂必有一個在區間[0，1]內，
從而知方程①在區間[0，2]上至少有一個實數解．
綜上所述，實數m的取值范圍為（-∞，-1]．
點評：本題主要考查集合間的包含關系，解題過程中用到了根與系數的關系，較好．