
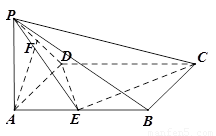
如圖,已知在四棱錐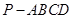 中,底面
中,底面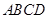 是矩形,
是矩形,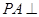 平面
平面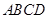 ,
,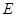 、
、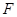 分別是
分別是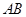 、
、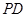 的中點(diǎn).
的中點(diǎn).
(Ⅰ)求證: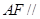 平面
平面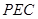 ;
;
(Ⅱ)若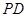 與平面
與平面 所成角為
所成角為 ,且
,且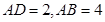 ,求點(diǎn)
,求點(diǎn)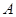 到平面
到平面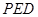 的距離.
的距離.
(1)見試題解析;(2) .
.
【解析】
試題分析:(I)要證明 平面
平面 ,關(guān)鍵是在平面
,關(guān)鍵是在平面 內(nèi)找到一條與直線
內(nèi)找到一條與直線 平行的直線,本題就想是否有一個(gè)過直線
平行的直線,本題就想是否有一個(gè)過直線 的平面與平面
的平面與平面 相交,交線就是我們要找的平行直線(可根據(jù)線面平行的性質(zhì)定理知),在圖形中可容易看出應(yīng)該就是平面
相交,交線就是我們要找的平行直線(可根據(jù)線面平行的性質(zhì)定理知),在圖形中可容易看出應(yīng)該就是平面 ,只不過再想一下,交線到底是什么而已,當(dāng)然具體輔助線的作法也可換成另一種說法(即試題解析中的直接取
,只不過再想一下,交線到底是什么而已,當(dāng)然具體輔助線的作法也可換成另一種說法(即試題解析中的直接取 中點(diǎn)
中點(diǎn) ,然后連接
,然后連接 的方法);(2)由于
的方法);(2)由于 平面
平面 ,所以三棱錐
,所以三棱錐 的體積可以很快求出,從而本題可用體積法求點(diǎn)
的體積可以很快求出,從而本題可用體積法求點(diǎn) 到平面
到平面 的距離,另外由于
的距離,另外由于 ,如果取
,如果取 中點(diǎn)
中點(diǎn) ,則有
,則有 ,從而可得
,從而可得 平面
平面 ,也即平面
,也即平面
 平面
平面 ,這時(shí)點(diǎn)
,這時(shí)點(diǎn) 到平面
到平面 的垂線段可很快作出,從而迅速求出結(jié)論.
的垂線段可很快作出,從而迅速求出結(jié)論.
試題解析:(I)證明:如圖,取 的中點(diǎn)
的中點(diǎn) ,連接
,連接 .
.

由已知得 且
且 ,
,
又 是
是 的中點(diǎn),則
的中點(diǎn),則 且
且 ,
, 是平行四邊形, ∴
是平行四邊形, ∴
又 平面
平面 ,
, 平面
平面
 平面
平面
(II)設(shè) 平面
平面 的距離為
的距離為 ,
,
【法一】:因 平面
平面 ,故
,故 為
為 與平面
與平面 所成角,所以
所成角,所以 ,
,
所以 ,
, ,又因
,又因 ,
, 是
是 的中點(diǎn)所以
的中點(diǎn)所以 ,
, ,
, .
.
作 于
于 ,因
,因 ,則
,則
 ,
,
則 ,
,
因 所以
所以
【法二】因 平面
平面 ,故
,故 為
為 與平面
與平面 所成角,所以
所成角,所以 ,
,
所以 ,
, ,又因
,又因 ,
, 是
是 的中點(diǎn)所以
的中點(diǎn)所以 ,
, ,
, .
.
作 于
于 ,連結(jié)
,連結(jié) ,因
,因 ,則
,則 為
為 的中點(diǎn),故
的中點(diǎn),故
所以 平面
平面 ,所以平面
,所以平面 平面
平面 ,作
,作 于
于 ,則
,則 平面
平面 ,所以線段
,所以線段 的長(zhǎng)為
的長(zhǎng)為 平面
平面 的距離.
的距離.
又 ,
,
所以 .
.
考點(diǎn):(1)線面平行的判定;(2)點(diǎn)到平面的距離.


 期末寶典單元檢測(cè)分類復(fù)習(xí)卷系列答案
期末寶典單元檢測(cè)分類復(fù)習(xí)卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知在四棱錐P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分別是AB、PD的中點(diǎn).
如圖,已知在四棱錐P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分別是AB、PD的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知在四棱錐P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如圖,已知在四棱錐P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<| π | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
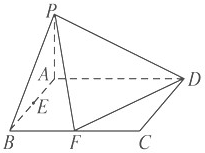 如圖,已知在四棱錐PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F(xiàn)分別是線段AB,BC的中點(diǎn).
如圖,已知在四棱錐PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F(xiàn)分別是線段AB,BC的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年貴州省六高三第一次考理科數(shù)學(xué)試卷(解析版) 題型:解答題
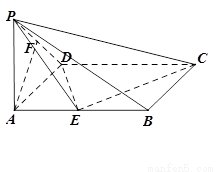
(本小題滿分12分)如圖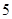 ,已知在四棱錐
,已知在四棱錐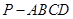 中,底面
中,底面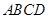 是矩形,
是矩形,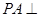 平面
平面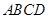 ,
,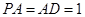 ,
,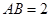 ,
,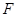 是
是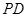 的中點(diǎn),
的中點(diǎn), 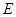 是線段
是線段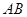 上的點(diǎn).
上的點(diǎn).
(I)當(dāng)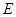 是
是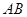 的中點(diǎn)時(shí),求證:
的中點(diǎn)時(shí),求證: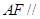 平面
平面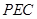 ;
;
(II)要使二面角 的大小為
的大小為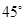 ,試確定
,試確定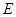 點(diǎn)的位置.
點(diǎn)的位置.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com