
1.在![]() 中,
中,![]() ,
,![]() .
.
(1)求角![]() ;
;
(2)設![]() ,求
,求![]() 的面積.
的面積.
 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
1(本小題滿分12分)
2008年為山東素質教育年,為響應素質教育的實施,某中學號召學生在放假期間至少參加一次社會實踐活動(以下簡稱活動).現統計了該校100名學生參加活動的情況,他們參加活動的次數統計如圖所示.
(1)求這些學生參加活動的人均次數;
(2)從這些學生中任選兩名學生,求他們參加活動次數恰好相等的概率;
 (3)從這些學生中任選兩名學生,用
(3)從這些學生中任選兩名學生,用![]() 表示這兩人參加活動次數之差的絕對值,求隨機變量
表示這兩人參加活動次數之差的絕對值,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省山一中高三熱身練文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)
在平面直角坐標系中,已知向量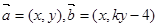 (
(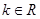 ),
),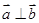 ,動點
,動點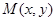 的軌跡為
的軌跡為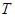 .
.
(1)求軌跡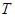 的方程,并說明該方程表示的曲線的形狀;
的方程,并說明該方程表示的曲線的形狀;
(2)當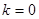 時,過點
時,過點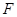 (0,1),作軌跡T的兩條互相垂直的弦
(0,1),作軌跡T的兩條互相垂直的弦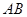 、
、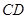 ,設
,設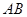 、
、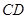 的中點分別為
的中點分別為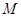 、
、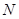 ,試判斷直線
,試判斷直線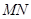 是否過定點?并說明理由.
是否過定點?并說明理由.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年海南省海口市高三高考調研考試理科數學 題型:解答題
(本小題滿分12分)
某市為了對學生的數理(數學與物理)學習能力進行分析,從10000名學生中隨機抽出100位學生的數理綜合學習能力等級分數(6分制)作為樣本,分數頻數分布如下表:
|
等級得分 |
|
|
|
|
|
|
|
人數 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等級分數大于4分作為良好的標準,從樣本中任意抽取2名學生,求恰有1名學生為良好的概率;
(Ⅱ)統計方法中,同一組數據常用該組區間的中點值(例如區間 的中點值為1.5)作為代表:
的中點值為1.5)作為代表:
(ⅰ)據此,計算這100名學生數理學習能力等級分數的期望 及標準差
及標準差 (精確到0.1);
(精確到0.1);
(ⅱ) 若總體服從正態分布,以樣本估計總體,估計該市這10000名學生中數理學習能力等級在 范圍內的人數 .
范圍內的人數 .
(Ⅲ)從這10000名學生中任意抽取5名同學,
他們數學與物理單科學習能力等級分
數如下表:


(ⅰ)請畫出上表數據的散點圖;
(ⅱ)請根據上表提供的數據,用最小二乘法求出 關于
關于 的線性回歸方程
的線性回歸方程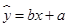 (附參考數據:
(附參考數據: )
)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年黑龍江哈爾濱市高三第三次模擬考試理科數學試卷(解析版) 題型:解答題
如圖,四棱柱 中,
中,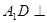 平面
平面 ,底面
,底面 是邊長為
是邊長為 的正方形,側棱
的正方形,側棱 .
.

(1)求三棱錐 的體積;
的體積;
(2)求直線 與平面
與平面 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一點
上存在一點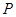 ,使得
,使得 ,當二面角
,當二面角 的大小為
的大小為 時,求實數
時,求實數 的值.
的值.
【解析】(1)在 中,
中,
 .
(3’)
.
(3’)
(2)以點D為坐標原點,建立如圖所示的空間直角坐標系 ,則
,則
 (4’)
(4’)
 ,設平面
,設平面 的法向量為
的法向量為 ,
,
由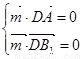 得
得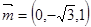 ,
(5’)
,
(5’)
則 ,
,
 . (7’)
. (7’)
(3)
設平面 的法向量為
的法向量為 ,由
,由 得
得 ,
(10’)
,
(10’)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com