
【題目】如圖,已知![]() 的兩頂點坐標(biāo)
的兩頂點坐標(biāo)![]() ,
,![]() ,圓
,圓![]() 是
是![]() 的內(nèi)切圓,在邊
的內(nèi)切圓,在邊![]() ,
,![]() ,
,![]() 上的切點分別為
上的切點分別為![]() ,
,![]() ,
,![]() ,
,![]() .
.
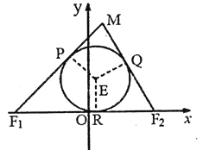
(Ⅰ)求證:![]() 為定值,并求出動點
為定值,并求出動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過![]() 的斜率不為零直線交曲線
的斜率不為零直線交曲線![]() 于
于![]() 、
、![]() 兩點,求證:
兩點,求證:![]() 為定值.
為定值.
【答案】(Ⅰ)證明詳見解析,曲線![]() 的方程為
的方程為![]() ;(Ⅱ)詳見解析.
;(Ⅱ)詳見解析.
【解析】
(Ⅰ)利用切線長相等可求得![]() ;根據(jù)橢圓定義可知動點
;根據(jù)橢圓定義可知動點![]() 的軌跡
的軌跡![]() 是以
是以![]() ,
,![]() 為焦點,長軸長為
為焦點,長軸長為![]() 的橢圓(不含橢圓與
的橢圓(不含橢圓與![]() 軸的交點),進(jìn)而求得結(jié)果;
軸的交點),進(jìn)而求得結(jié)果;
(Ⅱ)設(shè)![]() 的方程為
的方程為![]() ,與橢圓方程聯(lián)立得到韋達(dá)定理的形式,利用弦長公式求得
,與橢圓方程聯(lián)立得到韋達(dá)定理的形式,利用弦長公式求得![]() ,根據(jù)平面向量數(shù)量積運算求得
,根據(jù)平面向量數(shù)量積運算求得![]() ,進(jìn)而求得
,進(jìn)而求得![]() .
.
(Ⅰ)由題意得:![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() 動點
動點![]() 的軌跡
的軌跡![]() 是以
是以![]() ,
,![]() 為焦點,長軸長為
為焦點,長軸長為![]() 的橢圓(不含橢圓與
的橢圓(不含橢圓與![]() 軸的交點),
軸的交點),
設(shè)曲線![]() 方程為:
方程為:![]() ,
,
則![]() ,解得:
,解得:![]() ,又
,又![]() ,
,![]() ,
,
![]() 曲線
曲線![]() 的方程為
的方程為![]() ;
;
(Ⅱ)證明:由(Ⅰ)得:![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
![]() 直線
直線![]() 的斜率不為零,
的斜率不為零,![]() 可設(shè)
可設(shè)![]() 的方程為
的方程為![]() ,
,
聯(lián)立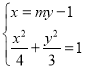 消去
消去![]() 并整理得:
并整理得:![]() ,
,
則![]() ,
,
![]() ,
,![]() ,
,
![]()
 ,
,
![]()
![]() ,
,
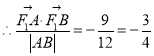 ,
, ,
,
綜上可得:![]() 為定值
為定值![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
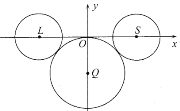
【題目】2020年是中國傳統(tǒng)的農(nóng)歷“鼠年”,有人用3個圓構(gòu)成“卡通鼠”的形象,如圖:![]() 是圓
是圓![]() 的圓心,圓
的圓心,圓![]() 過坐標(biāo)原點
過坐標(biāo)原點![]() ;點
;點![]() 、
、![]() 均在
均在![]() 軸上,圓
軸上,圓![]() 與圓
與圓![]() 的半徑都等于2,圓
的半徑都等于2,圓![]() 圓
圓![]() 均與圓
均與圓![]() 外切.已知直線
外切.已知直線![]() 過點
過點![]() .
.
(1)若直線![]() 與圓
與圓![]() 、圓
、圓![]() 均相切,則
均相切,則![]() 截圓
截圓![]() 所得弦長為__________;
所得弦長為__________;
(2)若直線![]() 截圓
截圓![]() 、圓
、圓![]() 、圓
、圓![]() 所得弦長均等于
所得弦長均等于![]() ,則
,則![]() __________.
__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 、拋物線
、拋物線![]() 的焦點均在
的焦點均在![]() 軸上,
軸上,![]() 的中心和
的中心和![]() 的頂點均為原點
的頂點均為原點![]() ,從每條曲線上取兩個點,將其坐標(biāo)記錄于下表中:
,從每條曲線上取兩個點,將其坐標(biāo)記錄于下表中:
| 3 |
| 4 |
|
|
| 0 |
|
|
(Ⅰ)求![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)請問是否存在直線![]() 滿足條件:①過
滿足條件:①過![]() 的焦點
的焦點![]() ;②與
;②與![]() 交不同兩點
交不同兩點![]() 且滿足
且滿足![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 件次品和
件次品和![]() 件正品混放在一起,現(xiàn)需要通過檢測將其區(qū)分,每次隨機(jī)檢測一件產(chǎn)品,檢測后不放回,直到檢測出
件正品混放在一起,現(xiàn)需要通過檢測將其區(qū)分,每次隨機(jī)檢測一件產(chǎn)品,檢測后不放回,直到檢測出![]() 件次品或者檢測出
件次品或者檢測出![]() 件正品時檢測結(jié)束.
件正品時檢測結(jié)束.
(1)求第一次檢測出的是次品且第二次檢測出的是正品的概率;
(2)已知每檢測一件產(chǎn)品需要費用![]() 元,設(shè)
元,設(shè)![]() 表示直到檢測出
表示直到檢測出![]() 件次品或者檢測出
件次品或者檢測出![]() 件正品時所需要的檢測費用(單位:元),求
件正品時所需要的檢測費用(單位:元),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近年電子商務(wù)蓬勃發(fā)展,現(xiàn)從某電子商務(wù)平臺評價系統(tǒng)中隨機(jī)選出200次成功交易,并對其評價進(jìn)行統(tǒng)計,統(tǒng)計結(jié)果顯示:網(wǎng)購者對商品的滿意率為0.70,對快遞的滿意率為0.60,其中對商品和快遞都滿意的交易為80次.
(1)根據(jù)已知條件完成下面的2×2列聯(lián)表,并回答在犯錯誤的概率不超過0.10的前提下,能否認(rèn)為“網(wǎng)購者對商品滿意與對快遞滿意之間有關(guān)系”?
對快遞滿意 | 對快遞不滿意 | 合計 | |
對商品滿意 | 80 | ||
對商品不滿意 | |||
合計 | 200 |
(2)為進(jìn)一步提高購物者的滿意度,平臺按分層抽樣方法從200次交易中抽取10次交易進(jìn)行問卷調(diào)查,詳細(xì)了解滿意與否的具體原因,并在這10次交易中再隨機(jī)抽取2次進(jìn)行電話回訪,聽取購物者意見.求電話回訪的2次交易至少有一次對商品和快遞都滿意的概率.
附: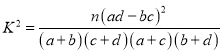 (其中
(其中![]() 為樣本容量)
為樣本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 經(jīng)過點
經(jīng)過點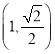 ,
,![]() ,
,![]() 是C的左、右焦點,過
是C的左、右焦點,過![]() 的直線l與C交于A,B兩點,且
的直線l與C交于A,B兩點,且![]() 的周長為
的周長為![]() .
.
(1)求C的方程;
(2)若![]() ,求l的方程.
,求l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙、丙三人投籃的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲與乙的命中率之和.若甲與乙各投籃一次,每人投籃相互獨立,則他們都命中的概率為0.18.
(1)求甲、乙、丙三人投籃的命中率;
(2)現(xiàn)要求甲、乙、丙三人各投籃一次,假設(shè)每人投籃相互獨立,記三人命中總次數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,![]() 的頂點
的頂點![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差數(shù)列.
成等差數(shù)列.
(1)求![]() 的頂點
的頂點![]() 的軌跡方程;
的軌跡方程;
(2)直線![]() 與頂點
與頂點![]() 的軌跡交于
的軌跡交于![]() 兩點,當(dāng)線段
兩點,當(dāng)線段![]() 的中點
的中點![]() 落在直線
落在直線![]() 上時,試問:線段
上時,試問:線段![]() 的垂直平分線是否恒過定點?若過定點,求出定點的坐標(biāo);若不過定點,請說明理由.
的垂直平分線是否恒過定點?若過定點,求出定點的坐標(biāo);若不過定點,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,以坐標(biāo)原點為極點,x軸正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為
中,以坐標(biāo)原點為極點,x軸正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為![]() ,曲線C的極坐標(biāo)方程為
,曲線C的極坐標(biāo)方程為![]() .
.
(Ⅰ)求直線l和曲線C的直角坐標(biāo)方程;
(Ⅱ)點M為曲線C上一點,求M到直線l的最小距離.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com