
(
吉林實驗中學模擬)如下圖,在正方體ABCD- 中,M是棱AB的中點.
中,M是棱AB的中點.
(1)
求證:BC∥平面 ;
;
(2)
求二面角 -
- -C的大小.
-C的大小.

|
解析:解法一: (1)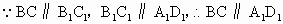 . .
又 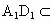 平面 平面 , ,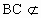 平面 平面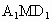 , ,
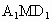 ; (5分) ; (5分)
(2) 設平面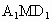 與棱DC相交于點N,連結 與棱DC相交于點N,連結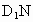 ,則點N是DC的中點. ,則點N是DC的中點.
 , ,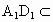 平面 平面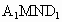 ,∴平面 ,∴平面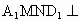 平面 平面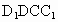 ,且 ,且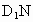 是交線. 是交線.
過點 C作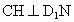 于H點,則CH⊥平面 于H點,則CH⊥平面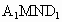 ,再過H作HO⊥ ,再過H作HO⊥ 于點O, 于點O,
連結 CO,根據三垂線定理得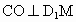 ,從而 ,從而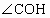 是二面角C- 是二面角C- -N,也就是所求二面角 -N,也就是所求二面角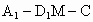 的補二面角的平面角. (8分) 的補二面角的平面角. (8分)
設正方體的棱長為 2,則在 中,由于 中,由于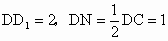 ,所以有 ,所以有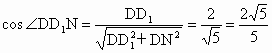 . .
在 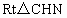 中,由于 中,由于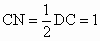 , ,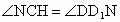 ,所以有 ,所以有
又由于可求得
所以在 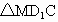 中,有 中,有
進而有 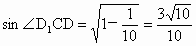 . .
根據三角形面積公式得
從而在 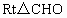 中, 中,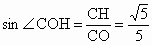 , ,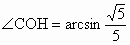 . .
因此所求的二面角 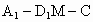 的大小為 的大小為 . (12分) . (12分)
解法二:分別以直線 DA、DC、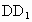 為x、y、z軸建立空間直角坐標系D-xyz,并設正方體的棱長為2,則相關點的坐標分別為 為x、y、z軸建立空間直角坐標系D-xyz,并設正方體的棱長為2,則相關點的坐標分別為 (2,0,2), (2,0,2),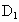 (0,0,2),C(0,2,0),M(2,1,0), (6分) (0,0,2),C(0,2,0),M(2,1,0), (6分)
設 n=(x,y,z)是平面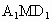 的法向量, 的法向量,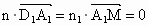 . .
而且 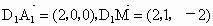 , ,
所以有  即 即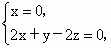
令 z=1,則y=2x,x=0,從而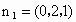 . (8分) . (8分)
再設 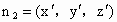 是平面 是平面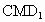 的法向量, 的法向量,
則 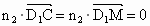 , ,
而且 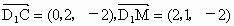 , ,
所以有 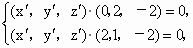 即 即
令 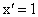 ,則 ,則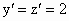 ,從而 ,從而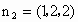 . .
設 θ是所求二面角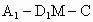 的平面角,則θ是鈍角,并且有 的平面角,則θ是鈍角,并且有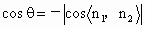 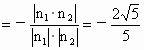 , ,
即 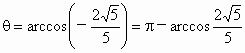 為所求. (12分) 為所求. (12分) |


科目:高中數學 來源: 題型:044
(
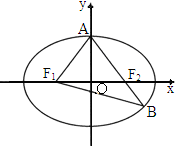
吉林實驗中學模擬)如圖所示,已知橢圓 (a>b>0),
(a>b>0), 、
、 分別為橢圓的左、右焦點,A為橢圓的上頂點,直線
分別為橢圓的左、右焦點,A為橢圓的上頂點,直線 交橢圓于另一點B.
交橢圓于另一點B.
(1)
若 ,求橢圓的離心率;
,求橢圓的離心率;
(2)
若橢圓的焦距為2,且 ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com