
| 1 |
| x |
| 1 |
| -x |
| 1 |
| x |
| 1 |
| x |


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
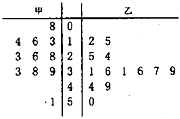 如圖是甲、乙兩名運動員每場得分的莖葉圖,中間的數字表示得分的十位數,旁邊的數字分別表示兩個人得分的個位數.從圖中得出的下列結論中,錯誤的一項是( )
如圖是甲、乙兩名運動員每場得分的莖葉圖,中間的數字表示得分的十位數,旁邊的數字分別表示兩個人得分的個位數.從圖中得出的下列結論中,錯誤的一項是( )查看答案和解析>>
科目:高中數學 來源: 題型:單選題
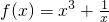 ,則f(x)是奇函數.
,則f(x)是奇函數.查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省巢湖市無為縣開城中學高一(上)第一次月考數學試卷(解析版) 題型:選擇題
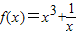 ,則f(x)是奇函數.
,則f(x)是奇函數.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com