
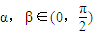 ,且tanα•tanβ<1,比較α+β與
,且tanα•tanβ<1,比較α+β與 的大小;
的大小;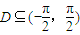 ,對任意的α、β∈D,當
,對任意的α、β∈D,當 時,恒有sinα<cosβ;并說明理由.
時,恒有sinα<cosβ;并說明理由. ,推出α+β與
,推出α+β與 的大小.
的大小. 內找出一個子區間,區間是固定的,也可以是變化的,對任意的α、β∈D,當
內找出一個子區間,區間是固定的,也可以是變化的,對任意的α、β∈D,當 時,恒有sinα<cosβ,利用函數的單調性,三角函數的符合特征,加以證明即可.
時,恒有sinα<cosβ,利用函數的單調性,三角函數的符合特征,加以證明即可.
 (2分)=>cos(α+β)>0(2分)
(2分)=>cos(α+β)>0(2分) (2分)
(2分) 或取
或取 等固定區間且D是
等固定區間且D是 的子集并說明理由者給(2分),
的子集并說明理由者給(2分), ,并說明理由者給(3分)
,并說明理由者給(3分) ,
, ,
, 或取
或取 等固定區間且D是
等固定區間且D是 的子集,且解答完整得(4分)
的子集,且解答完整得(4分) 的子集且區間的一端是變動者.且解答完整得(5分)
的子集且區間的一端是變動者.且解答完整得(5分) ,且解答完整得(6分)
,且解答完整得(6分)
 ,
, ,
, ,
, ,
, ,
, ,
, ,于是由α,β∈[γ1,γ2],
,于是由α,β∈[γ1,γ2], ,且
,且
 ,即:0<sinα<cosβ
,即:0<sinα<cosβ 或取
或取 等固定區間且D是
等固定區間且D是 的子集(兩端需異號),且解答完整得(6分)
的子集(兩端需異號),且解答完整得(6分) 的子集且區間的一端是變動者(兩端需異號).且解答完整得(7分)
的子集且區間的一端是變動者(兩端需異號).且解答完整得(7分) ,(γ1與γ2需異號)且解答完整得(8分)
,(γ1與γ2需異號)且解答完整得(8分) ,
, ,
, ,
,
 ,
, ,
, ,
, 為
為 ,
,

科目:高中數學 來源:2008-2009學年湖南省岳陽市岳化一中高一(下)6月月考數學試卷(解析版) 題型:解答題
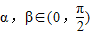 ,且tanα,tanβ是方程x2-5x+6=0的兩根.
,且tanα,tanβ是方程x2-5x+6=0的兩根.查看答案和解析>>
科目:高中數學 來源:2010年上海市奉賢區高考數學二模試卷(文科)(解析版) 題型:解答題
 ,且tanα•tanβ<1,比較α+β與
,且tanα•tanβ<1,比較α+β與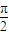 的大小;
的大小; ,對任意的α、β∈D,當
,對任意的α、β∈D,當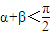 時,恒有sinα<cosβ;并說明理由.
時,恒有sinα<cosβ;并說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com