
【題目】設f(x)為奇函數,且在(﹣∞,0)內是減函數,f(2)=0,則 ![]() <0的解集為( )
<0的解集為( )
A.(﹣2,0)∪(2,+∞)
B.(﹣∞,2)∪(0,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0)∪(0,2)
科目:高中數學 來源: 題型:
【題目】某青少年成長關愛機構為了調研所在地區青少年的年齡與身高壯況,隨機抽取6歲,9歲,12歲,15歲,18歲的青少年身高數據各1000個,根據各年齡段平均身高作出如圖所示的散點圖和回歸直線![]() .根據圖中數據,下列對該樣本描述錯誤的是( )
.根據圖中數據,下列對該樣本描述錯誤的是( )
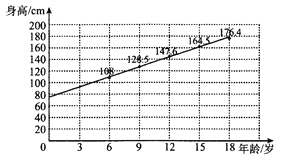
A. 據樣本數據估計,該地區青少年身高與年齡成正相關
B. 所抽取數據中,5000名青少年平均身高約為![]()
C. 直線![]() 的斜率的值近似等于樣本中青少年平均身高每年的增量
的斜率的值近似等于樣本中青少年平均身高每年的增量
D. 從這5種年齡的青少年中各取一人的身高數據,由這5人的平均年齡和平均身高數據作出的點一定在直線![]() 上
上
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E,F,G分別為A1B1 , BB1 , B1C1的中點,則AC1與D1E所成角的余弦值為 , AC1與平面EFG所成角的正弦值為 . 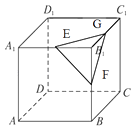
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() ,當點M(x,y)在y=f(x)的圖象上運動時,點N(x﹣2,ny)在函數y=gn(x)的圖象上運動(n∈N*).
,當點M(x,y)在y=f(x)的圖象上運動時,點N(x﹣2,ny)在函數y=gn(x)的圖象上運動(n∈N*).
(1)求y=gn(x)的表達式;
(2)若方程g1(x)=g2(x﹣2+a)有實根,求實數a的取值范圍;
(3)設 ![]() ,函數F(x)=H1(x)+g1(x)(0<a≤x≤b)的值域為
,函數F(x)=H1(x)+g1(x)(0<a≤x≤b)的值域為 ![]() ,求實數a,b的值.
,求實數a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1 , F2分別為雙曲線C: ![]() =1的左、右焦點,若存在過F1的直線分別交雙曲線C的左、右支于A,B兩點,使得∠BAF2=∠BF2F1 , 則雙曲線C的離心率e的取值范圍是( )
=1的左、右焦點,若存在過F1的直線分別交雙曲線C的左、右支于A,B兩點,使得∠BAF2=∠BF2F1 , 則雙曲線C的離心率e的取值范圍是( ) 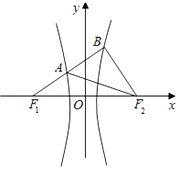
A.(3,+∞)
B.(1,2+ ![]() )
)
C.(3,2+ ![]() )
)
D.(1,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() .建立如圖所示的空間直角坐標系.
.建立如圖所示的空間直角坐標系.
(1)當![]() 時,求異面直線
時,求異面直線![]() 與
與![]() 的夾角的余弦值;
的夾角的余弦值;
(2)若二面角![]() 的平面角為
的平面角為![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 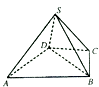
(Ⅰ)求證:SB=SD;
(Ⅱ)若∠BCD=120°,M為棱SA的中點,求證:DM∥平面SBC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com