
(本小題滿分15分)設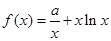 ,
,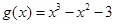 .
.
(1)當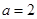 時,求曲線
時,求曲線 在
在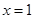 處的切線的斜率;
處的切線的斜率;
(2)如果存在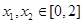 ,使得
,使得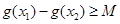 成立,求滿足上述條件的最大整數
成立,求滿足上述條件的最大整數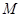 ;
;
(3)如果對于任意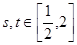 ,都有
,都有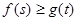 成立,求實數
成立,求實數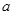 的取值范圍.
的取值范圍.
(1)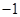 (2)
(2) (3)
(3)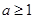
解析試題分析:(1)當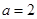 時,
時,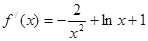 ,故
,故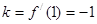 . ……3分
. ……3分
(2)存在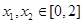 ,使得
,使得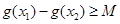 成立等價于
成立等價于 ,
,
∵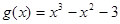 ,∴
,∴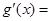
 ,
,
∴ 在
在 上單調遞減,在
上單調遞減,在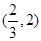 上單調遞增, ……6分
上單調遞增, ……6分
∴ ,
,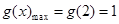 ,
,
∴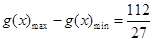 ,
,
∴滿足的最大整數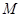 為4; ……8分
為4; ……8分
(3)對于任意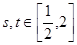 ,都有
,都有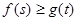 成立,等價于
成立,等價于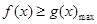 .
.
由(2)知,在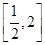 上,
上,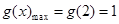 ,
,
∴在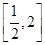 上,
上,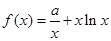
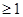 恒成立,等價于
恒成立,等價于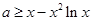 恒成立,
恒成立,
記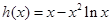 ,則
,則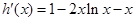 且
且 ,
,
∴當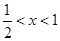 時,
時, ;當
;當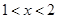 時,
時, ,
,
∴函數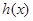 在
在 上單調遞增,在
上單調遞增,在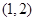 上單調遞減,
上單調遞減,
∴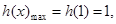 ∴
∴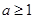 . ……15分
. ……15分
考點:本小題主要考查導數的幾何意義的應用和利用導數解決單調性、最值和恒成立等問題,考查學生綜
合運算所學知識分析問題、解決問題的能力和運算求解能力.
點評:恒成立問題是高考中一個常考的考點,恒成立問題一般轉化成最值問題來解決.導數是研究函數性
質尤其是單調性、最值問題的有力工具,要靈活運算,但是不要忘記定義域.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分13分))
京廣高鐵于2012年12月26日全線開通運營,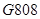 次列車在平直的鐵軌上勻速行駛,由于遇到緊急情況,緊急剎車時列車行駛的路程
次列車在平直的鐵軌上勻速行駛,由于遇到緊急情況,緊急剎車時列車行駛的路程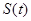 (單位:
(單位: )和時間
)和時間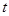 (單位:
(單位: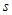 )的關系為:
)的關系為: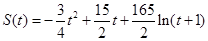 .
.
(1)求從開始緊急剎車至列車完全停止所經過的時間;
(2)求列車正常行駛的速度;
(3)求緊急剎車后列車加速度絕對值的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)設函數f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是單調函數,求a的取值范圍;
(2)若a=2,且當x∈[1,2]時,f(x)≤m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)定義在實數R上的函數y= f(x)是偶函數,當x≥0時,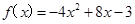 .
.
(Ⅰ)求f(x)在R上的表達式;
(Ⅱ)求y=f(x)的最大值,并寫出f(x)在R上的單調區間(不必證明).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
燕子每年秋天都要從北方飛到南方過冬。研究燕子的科學家發現,兩歲燕子的飛行速度可以表示為函數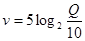 ,單位是
,單位是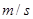 ,其中
,其中 表示燕子的耗氧量。
表示燕子的耗氧量。
(1)計算:兩歲燕子靜止時的耗氧量是多少個單位?(5分)
(2)當一只兩歲燕子的耗氧量是80個單位時,它的飛行速度是多少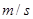 ?(5分)
?(5分)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)
提高過立交橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,成都某立交橋上的車流速度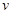 (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度 (單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當
(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當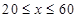 時,車流速度
時,車流速度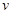 是車流密度
是車流密度 的一次函數.
的一次函數.
(Ⅰ)當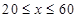 時,求函數
時,求函數 的表達式;
的表達式;
(Ⅱ)當車流密度 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)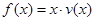 可以達到最大,并求出最大值.(精確到1輛/小時)
可以達到最大,并求出最大值.(精確到1輛/小時)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)已知集合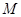 是滿足下列性質的函數
是滿足下列性質的函數 的全體:在定義域內存在
的全體:在定義域內存在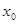 ,使得
,使得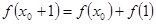 成立。
成立。
(Ⅰ)函數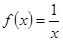 是否屬于集合
是否屬于集合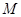 ?說明理由;
?說明理由;
(Ⅱ)設函數 ,求
,求 的取值范圍;
的取值范圍;
(Ⅲ)設函數 圖象與函數
圖象與函數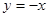 的圖象有交點,
的圖象有交點,
證明:函數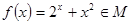 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分13分)某產品生產廠家根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品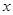 (百臺),其總成本為
(百臺),其總成本為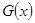 (萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為2萬元(總成本=固定成本+生產成本).銷售收入
(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為2萬元(總成本=固定成本+生產成本).銷售收入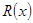 (萬元)滿足
(萬元)滿足 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
(1)寫出函數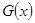 的解析式;
的解析式;
(2)寫出利潤函數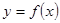 的解析式(利潤=銷售收入—總成本);
的解析式(利潤=銷售收入—總成本);
(3)工廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com