
【題目】某學校運動會的立定跳遠和30秒跳繩兩個單項比賽分成預賽和決賽兩個階段.下表為10名學生的預賽成績,其中有三個數據模糊.
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳遠 (單位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳繩 (單位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
在這10名學生中,進入立定跳遠決賽的有8人,同時進入立定跳遠決賽和30秒跳繩決賽的有6人,則( )
A. 2號學生進入30秒跳繩決賽 B. 5號學生進入30秒跳繩決賽
C. 8號學生進入30秒跳繩決賽 D. 9號學生進入30秒跳繩決賽
科目:高中數學 來源: 題型:
【題目】某少數民族的刺繡有著悠久的歷史,下圖![]() 為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含
為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含![]() 個小正方形.
個小正方形.
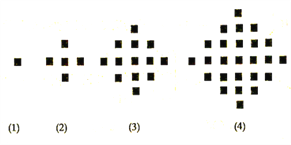
(1)求出![]() ;
;
(2)利用合情推理的“歸納推理思想”歸納出![]() 與
與![]() 的關系式,
的關系式,
(3)根據你得到的關系式求![]() 的表達式
的表達式
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 為常數,
為常數,![]() ).(Ⅰ)求函數
).(Ⅰ)求函數![]() 的單調區間;(Ⅱ)當
的單調區間;(Ⅱ)當![]() 時,是否存在實數
時,是否存在實數![]() ,使得當
,使得當![]() 時,不等式
時,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范圍;如果不存在,請說明理由(其中
的取值范圍;如果不存在,請說明理由(其中![]() 是自然對數的底數,
是自然對數的底數,![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】鹽化某廠決定采用以下方式對某塊鹽池進行開采:每天開采的量比上一天減少![]() ,10天后總量變為原來的一半,為了維持生態平衡,剩余總量至少要保留原來的
,10天后總量變為原來的一半,為了維持生態平衡,剩余總量至少要保留原來的![]() ,已知到今天為止,剩余的總量是原來的
,已知到今天為止,剩余的總量是原來的![]() .
.
(1)求![]() 的值;
的值;
(2)到今天為止,工廠已經開采了幾天?
(3)今后最多還能再開采多少天?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .現提供
.現提供![]() 的大致圖像的8個選項:
的大致圖像的8個選項:
(A)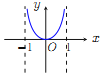 (B)
(B)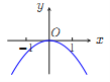 (C)
(C) (D)
(D)
(E) (F)
(F)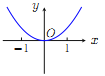 (G)
(G)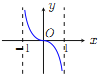 (H)
(H)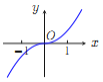
(Ⅰ)請你作出選擇,你選的是( );
(Ⅱ)對于函數圖像的判斷,往往只需了解函數的基本性質.為了驗證你的選擇的正確性,請你解決下列問題:
①![]() 的定義域是 ;
的定義域是 ;
②就奇偶性而言, ![]() 是 ;
是 ;
③當![]() 時,
時, ![]() 的符號為正還是負?并證明你的結論.
的符號為正還是負?并證明你的結論.
(解決了上述三個問題,你要調整你的選項,還來得及.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出x(單位:百萬元)與銷售額y(單位:百萬元)之間有如下的對應數據:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)畫出散點圖;
(2)求y關于x的線性回歸方程。
(3)如果廣告費支出為一千萬元,預測銷售額大約為多少百萬元?
參考公式
用最小二乘法求線性回歸方程系數公式: ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】做投擲2個骰子試驗,用(x,y)表示點P的坐標,其中x表示第1個骰子出現的點數,y表示第2個骰子出現的點數.
(1)求點P在直線y=x上的概率.
(2)求點P不在直線y=x+1上的概率.
(3)求點P的坐標(x,y)滿足16<x2+y2≤25的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知三棱錐P-ABC,∠ACB=90°,CB=4,AB=20,D為AB的中點,且△PDB是正三角形,PA⊥PC.
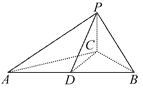
(1)求證:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com